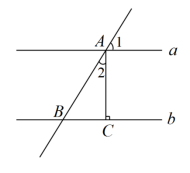
如图,直线 ,直线 c 与直线 a , b 分别相交于点 A , B ,
,垂足为 C .若
,则
( )
A . 52° B . 45° C . 38° D . 26°
答案
C
【分析】根据平行线的性质可得 ∠ ABC =52° ,根据垂直定义可得 ∠ ACB =90° ,然后利用直角三角形的两个锐角互余,进行计算即可解答.
【详解】解: ∵ a b ,
∴∠1=∠ ABC =52° ,
∵ AC ⊥ b ,
∴∠ ACB =90° ,
∴∠2=90°-∠ ABC =38° ,
故选: C .
【点睛】本题考查了平行线的性质,垂线,熟练掌握平行线的性质是解题的关键.