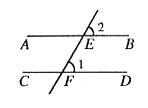
两直线平行，一组同位角的角平分线互相平行．（ ____ ）（填 “√”“×” ）

答案

√

【分析】写出已知求证进行证明即可得到结论．

【详解】已知：直线 AB 平行于直线 CD ，直线 EF 交直线 AB 与 M ，交直线 CD 于 F ，且 MQ 平分 ∠ EMB ， FG 平分 ∠ EFD ，

求证：

证明： ∵ ，

∴∠ EMB =∠ EFD ，

∵ MQ 平分 ∠ EMB ， FG 平分 ∠ EFD ，

∴ ，

∴ ，

∴

故答案为： √ ．

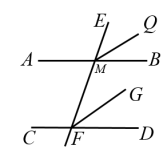
【点睛】此题考查了平行线的判定及性质，正确掌握平行线的判定定理及性质定理并解决问题是解题的关键．