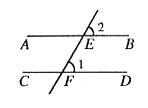
将一个直角三角板和一把直尺如图放置，如果 ，则 的度数是（ ）

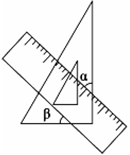
A ． 43° B ． 47° C ． 30° D ． 45°

答案

B

【分析】如图：延长 BC 交刻度尺的一边于 D 点，再利用平行线的性质、对顶角的性质，将已知角与所求角转化到 Rt△ CDE 中，最后利用三角形内角和定理求解即可．

【详解】解：如图，延长 BC 交刻度尺的一边于 D 点，

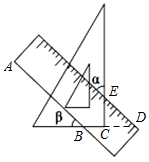
∵ AB DE ，

∴∠ β ＝ ∠ EDC ，

又 ∵∠ CED ＝ ∠ α ＝ 43° ， ∠ ECD ＝ 90° ，

∴∠ β ＝ ∠ EDC ＝ 90° ﹣ ∠ CED ＝ 90° ﹣ 46° ＝ 47° ．

故选： B ．

【点睛】本题主要考查了平行线的性质、三角形内角和定理等知识点，根据题意作出辅助线，构造出平行线是解答本题的关键．