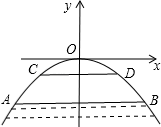
如图，有一座抛物线形拱桥，在正常水位时水面 AB 的宽为 20m ，如果水位上升 3m 水面 CD 的宽是 10m ．

(1) 求此抛物线的函数表达式．

(2) 在正常水位时，有一艘宽 8m 、高 2.5m 的小船，它能通过这座桥吗？

(3) 现有一艘船以每小时 5km 的速度向此桥径直驶来，当船距此桥 35km 时，桥下水位正好在 AB 处，之后水位每小时上涨 0.25m ，当水位在 CD 处时，将禁止船只通行．如果该船按原来的速度行驶，能否安全通过此桥？

答案

(1)

(2) 能安全通过，理由见详解

(3) 能安全通过，理由见详解

【分析】（ 1 ）设抛物线的解析式为： ，由 AB =20 ， CD =10 ，可得 B 点的横坐标为 10 ， D 点的横坐标为 5 ，设 D 点的纵坐标为 n ，则 C (5 ， n ) ，根据水面 CD 相对于水面 AB 升高了 3 m ，可得有 B 点的纵坐标为 n -3 ，即 B (10, n -3) ，将 B (10, n -3) 、 C (5, n ) 代入 中，即可求解；

（ 2 ）先得到 B (10,-4) 、 C (5,-1) ，由常识可知，小船经由水面的正中间航行，最有可能穿过小桥，当 x =8÷2=4 时， ，根据 -0.64-2.5=-3.14 ， -3.14 ＞ -4 ，即可判断；

（ 3 ）求出小船到达小桥时水面的水位即可作答．

（ 1 ）

由抛物线的图象在坐标系中的位置可知，抛物线的顶点在原点，

即设抛物线的解析式为： ，

∵ AB =20 ， CD =10 ，

∴ B 点的横坐标为 10 ， D 点的横坐标为 5 ，

设 D 点的纵坐标为 n ，则 C (5 ， n ) ，

∵ 水面 CD 相对于水面 AB 升高了 3 m ，

∴ 有 B 点的纵坐标为 n -3 ，即 B (10 ， n -3) ，

将 B (10 ， n -3) 、 C (5 ， n ) 代入 中，

有： ，

解得： ，

∴ 抛物线的解析式为： ；

（ 2 ）

根据（ 1 ）中 n 的值，可得 B (10,-4) 、 C (5,-1) ，

由常识可知，小船经由水面的正中间航行，最有可能穿过小桥，

∵ 小船宽 8m ，船高 2.5m ，

∴ 当 x =8÷2=4 时， ，

∴-0.64-2.5=-3.14 ，

∵-3.14 ＞ -4 ，

∴ 小船可以通过这座桥，

即小船可以通过这座桥；

（ 3 ）

小船到达小桥所需的时间为： 35÷5=7 h ，

7 小时内水位上涨： 0.25×7=1.75 m ，

∵ 水面 CD 相对于水面 AB 升高了 3 m ， 1.75 ＜ 3 ，

∴ 此时水位没有涨至 CD 处，

∴ 小船到达小桥时，航线依旧保持通行，

∴ 小船可以安全通过此桥．

【点睛】本题主要考查了抛物线的图象与性质以及求解抛物线解析式的知识．结合图象设抛物线的解析式为： ，是解答本题的关键．