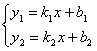直线 y ＝ x + n 与直线 y ＝ mx +3 n （ m 是常数， m ≠0 且 m ≠1 ）交于点 A ，当 n 的值发生变化时，点 A 到直线 y ＝ x ﹣ 3 的距离总是一个定值，则 m 的值是（　　）

A ． 3 B ． 2 C ． D ．

答案

C

【分析】先求得交点 A 的坐标，即可求出点 A 的轨迹，进而判断出直线 与直线 y ＝ x ﹣ 3 平行，即可求出 m 的值．

【详解】解： ∵ 直线 y ＝ x + n 与直线 y ＝ mx +3 n （ m 是常数， m ≠0 且 m ≠1 ）交于点 A ，

解析式联立解得， x ＝ ， y ＝ ，

∴ A （ ， ），

∴ yA ＝ xA ，

当 m 为一个的确定的值时， yA 是 xA 的正比例函数，

即：点 A 在直线 y ＝ x 上，

∵ 点 A 到直线 y ＝ x ﹣ 3 的距离总是一个定值，

∴ 直线 y ＝ x 与直线 y ＝ x ﹣ 3 平行，

∴ ＝ ，

∴ m ＝ ．

故选： C ．

【点睛】本题主要考查了一次函数图象上点的坐标特征，平行线的判定，得出点 A 的轨迹，利用方程的思想解决问题是解本题的关键．