如图,在射线 MB 上, MB =10 , A 是射线外一点, AB =5 ,且 A 到射线 MB 的距离 AC =3 ,动点 P 从点 M 出发,沿射线 MB 方向以 1 个单位 / 秒的速度运动,设点 P 运动的时间为 t 秒.解答下列问题.
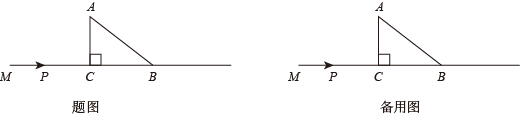
(1) 当 t 为何值时, △ PAB 是等腰三角形;
(2) 当 t 为何值时, △ PAB 是直角三角形.
答案
(1) t =5 或 15 或 2 或
(2) t =6 或
【分析】( 1 )在 Rt △ ABC 中, AB =5 , AC =3 ,由勾股定理可得 BC =4 , MP = t .分三种情况 ① BA = BP , ② AB = AP , ③ PA = PB 分别进行讨论即可;
( 2 )由 ,
,可得
,分两种情况: ① 当
, ② 当
时,分别进行讨论即可.
( 1 )
( 1 )在 Rt △ ABC 中, AB =5 , AC =3 ,由勾股定理可得 BC =4 , MP = t .下分三种情况
① 若 BA = BP ,如图 1
则有 ,解得
或 15 ;
② 若 AB = AP ,如图 2
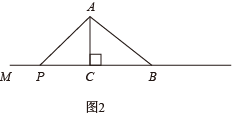
则有 PB =2 BC ,故有 ,解得
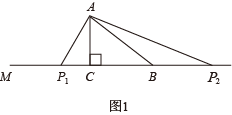
③ 若 PA = PB ,如图 3
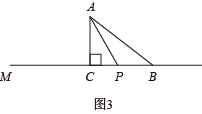
则有 ,解得
.
综上,当 t 为 5 或 15 或 2 或 时, △ PAB 是等腰三角形.
( 2 )
解:由 ,
,可得
下分两种情况:
① 当 时,如图 4
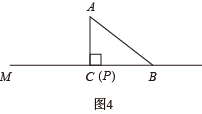
点 P 与点 C 重合,则
② 当 时,如图 5
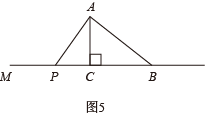
则有 ,解得
.
综上,当 t 为 6 或 时, △ PAB 是直角三角形.
【点睛】本题考查勾股定理及其逆用,分类讨论思想,能够根据题意进行分类讨论是解决本题的关键.

 。
。