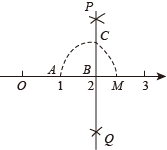
如图,数轴上点 A 、 B 分别对应 1 、 2 ,过点 B 作 PQ ⊥ AB ,以 B 为圆心, AB 长为半径画弧,交 PQ 于点 C ,以原点 O 为圆心, OC 长为半径画弧,交数轴于点 M ,则点 M 对应的数是( )
A . B .
C .
D .
答案
D
【分析】由题意易知 OB =2 , BC =1 ,然后根据勾股定理可得 ,进而问题可求解.
【详解】解:由题意得: OB =2 , BC =1 ,连接 OC ,如图,
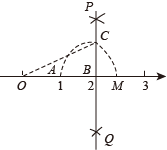
∵∠ OBC =90° ,
∴ ,
∴ 点 M 对应的数是 ;
故选: D .
【点睛】本题主要考查勾股定理,熟练掌握勾股定理是解题的关键.
