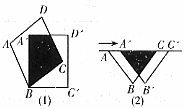
如图,边长为 的正方形
内接于
,
,
分别与
相切于点
和点
,
的延长线与
的延长线交于点
,则图中阴影部分的面积为( )

A . B .
C .
D .
答案
C
【分析】根据正方形的性质以及切线的性质,求得 的长,勾股定理求得
的长,进而根据
即可求解.
【详解】如图,连接 ,
,

边长为
的正方形
内接于
,即
,
,
,
为
的直径,
,
,
分别与
相切于点
和点
,
,
四边形
是正方形,
,
是等腰直角三角形,
,
,
四边形
是矩形,
,
四边形
是正方形,
,
,
.
故选 C .
【点睛】本题考查了圆的切线的性质,正方形的性质,勾股定理,等腰直角三角形的性质,掌握以上知识是解题的关键.