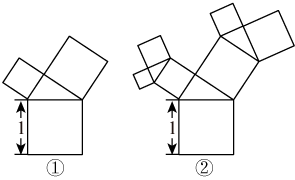
有一个面积为 1 的正方形，经过一次 “ 生长 ” 后，在它的左右肩上生出两个小正方形（如图 ① ），其中，三个正方形围成的三角形是直角三角形，再经过一次 “ 生长 ” 后，生出了 4 个正方形（如图 ② ），如果按此规律继续 “ 生长 ” 下去，那么它将变得 “ 枝繁叶茂 ” ．在 “ 生长 ” 了 2022 次后形成的图形中所有正方形的面积和是（ ）

A ． 2021 B ． 2022 C ． 2023 D ． 2024

答案

C

【分析】根据题目可知 “ 生长 ”1 次后，所有正方形的面积和是 2×1=2 ； “ 生长 ”2 次后，所有的正方形的面积和是 3×1=3 ，探究规律求出 “ 生长 ”2022 次后形成图形中所有正方形的面积之和即可．

【详解】解：由勾股定理知：

图 ① 中生长出的两个正方形面积和等于原来正方形的面积，所有正方形的面积和为 2 ；

同样图 ② 中生长出的四个正方形面积和等于图 ① 中生长出的两个正方形的面积之和，所有正方形的面积和为 3 ；

…… ，

经过 n 次 “ 生长 ” 后形成的图形中所有正方形的面积和是 n +1 ；

经过 2022 次 “ 生长 ” 后形成的图形中所有正方形的面积和是 2023 ．

故选： C ．

【点睛】本题考查勾股定理，其中能够根据勾股定理发现每一次得到的新的正方形的面积和与原正方形的面积之间的关系是解本题的关键．