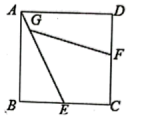
如图，正方形 ABCD 的边长为 6 ，点 E ， F 分别是边 BC 和 CD 的中点，连接 AE ，在 AE 上取点 G ，连接 GF ，若 ，则 GF 的长为（ ）

A ． B ． C ． D ．

答案

C

【解析】

【分析】

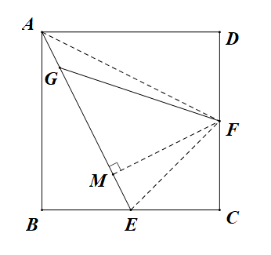
根据已知条件，连接 AF 、 EF ，过点 F 作 FM ⊥ AE ，垂足为 M ，构造关于 GF 的直角三角形，解直角三角形即可求出 GF 的长．

【详解】

解：如图，连接 AF 、 EF ，过点 F 作 FM ⊥ AE ，垂足为 M ，

∵ 正方形 ABCD 边长为 6 ，点 E 、 F 分别是 BC 、 CD 的中点，

∴ AB ＝ BC ＝ CD ＝ AD ＝ 6 ， BE ＝ CE ＝ CF ＝ DF ＝ 3 ，

， ，

＝ 6 ² － ×3×6 － ×3×6 － ×3×3

＝ ，

又 ∵

＝ ×3 × FM ，

即 ×3 × FM ＝ ，解得 FM ＝ ．

∵ ，

∴ 是等腰直角三角形， GM ＝ FM ＝ ，

∴ ．

故选： C ．

【点睛】

本题考查直角三角形的相关计算，构造关于 GF 的直角三角形、利用勾股定理，是解题的关键．