定义:在平面直角坐标系中,对于任意两点 ,
,如果点
满足
,
,那么称点 M 是点 A 、 B 的 “ 双减点 ” .
例如: ,
、当点
满足
,
,则称点
是点 A 、 B 的 “ 双减点 ” .
(1) 写出点 ,
的 “ 双减点 ” C 的坐标;
(2) 点 ,点
,点
是点 E 、 F 的 “ 双减点 ” .求 y 与 x 之间的函数关系式;
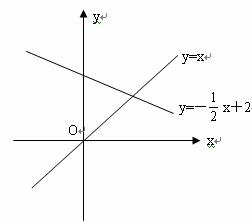
(3) 在( 2 )的条件下, y 与 x 之间的函数图象与 y 轴、 x 轴分别交于点 A 、 C 两点, B 点坐标为 ,若点 E 在平面直角坐标系内,在直线 AC 上是否存在点 F ,使以 A 、 B 、 E 、 F 为顶点的四边形为菱形?若存在,请求出 F 点的坐标;若不存在,请说明理由.
答案
(1)
(2)
(3) 存在, 点的坐标为
或
或
【解析】
【分析】
( 1 )设 ,根据 “ 双减点 ” 的定义求解即可;
( 2 )根据 “ 双减点 ” 的定义求解可得 表示的
,消元求解即可;
( 3 )由 y 与 x 之间的函数关系式求出 的坐标,可知
是等腰三角形,根据菱形的性质,以 A 、 B 、 E 、 F 为顶点的四边形为菱形时,有三种情况,如图所示, ①
为菱形
的边长,则
,作
于
,
于
,根据
,求出
的值,在
中,由勾股定理得
,求出
的值,进而可得
的值,证明
,有
,求出
的值,进而得到
的值,即可得到
点坐标; ②
为菱形
的对角线,则
,可得
点坐标; ③
为菱形
的对角线,则
,
是线段
的中点,进而可求
点坐标.
(1)
解:设
由题意知 ,
∴ .
(2)
解:由题意得 ,
解得
将 代入
中得
整理得 y 与 x 之间的函数关系式为 .
(3)
解:存在.
∵
∴ 当 时,
,
当 时,
,
在 中,由勾股定理得
∵
∴
由题意得,以 A 、 B 、 E 、 F 为顶点的四边形为菱形时,有三种情况,如图所示,
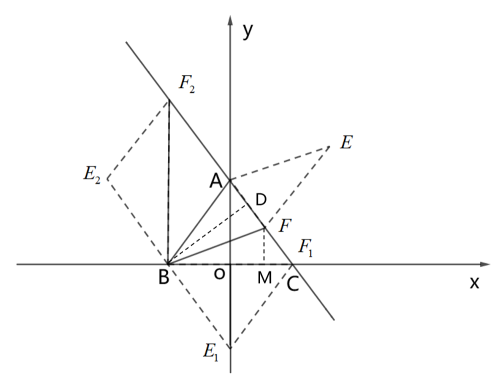
① 为菱形
的边长,则
,作
于
,
于
∵ 即
解得
在 中,由勾股定理得
∴ ,
∵
∴
∴ 即
解得 ,
∴
∴ ;
② 为菱形
的对角线,则
∴ ;
③ 为菱形
的对角线,则
∵
∴ 是线段
的中点
∴ ;
综上所述,直线 AC 上存在点 F ,使以 A 、 B 、 E 、 F 为顶点的四边形为菱形, F 点的坐标为 或
或
.
【点睛】
本题考查了新定义下点坐标的运算,一次函数解析式,菱形的性质,勾股定理,相似三角形的判定与性质.解题的关键在于熟练掌握菱形的性质.