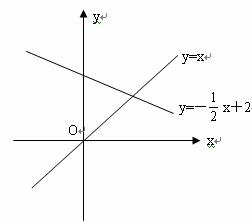
在平面直角坐标系 xOy 中，直线 y = x +2 与 x 轴交于点 A ，与过点 B （ 0 ， 1 ）且平行于 x 轴的直线 l 交于点 C ，点 A 关于直线 l 的对称点为点 D ．

(1) 求点 C 、 D 的坐标；

(2) 将直线 y = x +2 在直线 l 下方的部分和线段 CD 记为一个新的图象 G ．若直线 y =2 x + b 与图象 G 有两个公共点，结合函数图象，求 b 的取值范围．

答案

(1) C （﹣ 1 ， 1 ）， D （ -2 ， 2 ）

(2)3 ＜ b ≤6 ．

【解析】

【分析】

（ 1 ）令 y ＝ 0 求出点 A 坐标，利用轴对称的性质即可得出点 D 坐标；由直线 y ＝ x +2 与过点 B （ 0 ， 2 ）且平行于 x 轴的直线 l 交于点 C 即可得出点 C 坐标；

（ 2 ）结合图象可得当直线 y ＝ 2 x + b 经过点 C 和点 D 时是 b 的取值的临界情况，分别求出此时 b 的取值就可以得到 b 的范围．

(1)

解： ∵ 直线 y ＝ x +2 与 x 轴交于点 A ，

∴ A （﹣ 2 ， 0 ）

∵ 直线 y ＝ x +2 与过点 B （ 0 ， 1 ）且平行于 x 轴的直线 l 交于点 C ，

∴ C （﹣ 1 ， 1 ）

∵ 点 A 关于直线 l 的对称点为点 D ，

∴ D （ -2 ， 2 ）

(2)

解：如图：

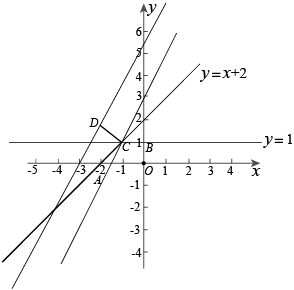
当直线 y ＝ 2 x + b 经过点 C （﹣ 1 ， 1 ）时，

∴1 ＝ 2× （﹣ 1 ） + b ，

解得 b ＝ 3

当直线 y ＝ 2 x + b 经过点 D （﹣ 2 ， 2 ）时，

∴2 ＝ 2× （﹣ 2 ） + b ，

解得 b ＝ 6

∴ b 的取值范围为 3 ＜ b ≤6 ．

【点睛】

本题考查了一次函数的图象与性质以及两直线相交或平行问题；解题的关键是结合图象进行作答．