如图，点A（﹣1，

当前位置：

学科首页

八下第十九章一次函数

一次函数

试题详情

难度：

使用次数：264

更新时间：2022-03-29

纠错

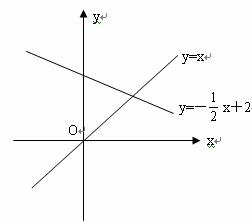
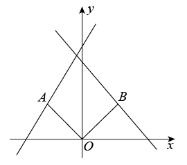
如图，点 A （﹣ 1 ， m ）在直线 y =2 x +3 上，连结 OA ， ∠ AOB =90° ，点 B 在直线 y = ﹣ x + b 上， OA = OB ，则 b =________ ．

查看答案

题型：填空题

知识点：一次函数

下载试题

复制试题

【答案】

【解析】

【分析】

先把点 A 坐标代入直线 y =2 x +3 ，得出 m 的值，然后得出点 B 的坐标，再代入直线 y =- x + b 解答即可．

【详解】

解：把 A （ -1 ， m ）代入直线 y =2 x +3 ，可得： m =-2+3=1 ，

因为 ∠ AOB =90° ， OA = OB ，

所以线段 OA 绕点 O 顺时针旋转 90° ，得线段 OB ，所以点 B 的坐标为（ 1 ， 1 ），

把点 B 代入直线 y =- x + b ，可得： 1=-1+ b ， ∴ b =2 ，

故答案为： 2 ．

【点睛】

此题考查一次函数图象上点的坐标特征，旋转中的坐标变换 . 关键是根据题意，利用旋转中的坐标变换规律求点的坐标．

考点梳理:

根据可圈可点权威老师分析，试题“ ”主要考查你对变量及函数等考点的理解。关于这些考点的“资料梳理”如下：

◎ 变量及函数的定义

函数：一般地，在一个变化过程中，如果有两个自变量x与y，并且对于x的每一个确定的值，y都有唯一确定的值与其对应，那么我们就说x是自变量，y是x的函数。
如果当x=a时，y=b，那么b叫做当自变量的值为a时的函数值。
变量：
在一个变化过程中，我们称数值发生变化的量为变量。（数学中，常常为x，而y则随x值的变化而变化），有些数值是不随变量而改变的，我们称它们为常量。
自变量：函数一个与它量有关联的变量，这一量中的任何一值都能在它量中找到对应的固定值。
因变量(函数)：随着自变量的变化而变化，且自变量取唯一值时，因变量(函数)有且只有唯一值与其相对应。

◎ 变量及函数的知识扩展

1、变量：在一个变化过程中，我们称数值发生变化的量为变量。
2、函数：一般地，在一个变化过程中，如果有两个自变量x与y，并且对于x的每一个确定的值，y都有唯一确定的值与其对应，那么我们就说x是自变量，y是x的函数。
如果当x=a时，y=b，那么b叫做当自变量的值为a时的函数值。

◎ 变量及函数的特性

变量的关系：
在具体情境中，感受两个变量之间的关系，就是一个变量随着另一个变量的变化情况，例如随着一个变量的变化，有的变量是呈匀速变化的，有的变量是呈不匀速变化的；
进而发现实际情景中的变量及其相互关系，并确定其中的自变量和因变量，会用运动变化的基本观点观察事物。也就是说，在两个有相依关系的变量中，其中一个是自变量，另一个是因变量；
自变量和因变量之间的变化关系可以用表格来刻画，也可以用图象来描述，并能对未来的趋势加以预测。

◎ 变量及函数的知识点拨

函数自变量的取值范围的确定：
使函数有意义的自变量的取值的全体，叫做函数自变量的取值范围．
自变量的取值范围的确定方法：
首先要考虑自变量的取值必须使解析式有意义，
①当解析式为整式时，自变量的取值范围是全体实数；
②当解析式是分数的形式时，自变量的取值范围是使分母不为零的所有实数；
③当解析式中含有平方根时，自变量的取值范围是使被开方数不小于零的实数；
④当函数解析式表示实际问题时，自变量的取值必须使实际问题有意义。

◎ 变量及函数的教学目标

1、通过探索具体问题中的数量关系和变化规律来了解常量、变量的意义；
2、学会用含一个变量的代数式表示另一个变量；
3、结合实例，理解函数的概念以及自变量的意义；在理解掌握函数概念的基础上，确定函数关系式；
4、会根据函数解析式和实际意义确定自变量的取值范围。

◎ 变量及函数的考试要求

能力要求：知道
课时要求：40
考试频率：选考
分值比重：2

开通会员

登录并加入会员可无限制查看知识点解析

类题推荐：

一次函数

难度：

使用次数：158

更新时间：2021-07-13

加入组卷

李老师给出了一个函数，甲、乙、丙三位学生分别指出这个函数的一个特征．甲：它的图像经过第一象限；乙：它的图像也经过第二象限；丙：在第一象限内函数值y随x增大而增大．在你学过的函数中，写出一个满足上述特征的函数解析式　　．

查看答案

题型：填空题

知识点：一次函数

复制

试题详情

纠错

难度：

使用次数：463

更新时间：2009-02-19

加入组卷

某农户种植一种经济作物，总用水量（米）与种植时间（天）之间的函数关系式如图10所示．

（1）第天的总用水量为多少米？

（2）当时，求与之间的函数关系式．

（3）种植时间为多少天时，总用水量达到7000米？

查看答案

题型：计算题

知识点：一次函数

复制

试题详情

纠错

难度：

使用次数：159

更新时间：2021-07-13

加入组卷

如下图，在平行四边形ABCD中，∠DAB＝60°，AB＝5，BC＝3，点P从起点D出发，沿DC、CB向终点B匀速运动。设点P所走过的路程为x，点P所经过的线段与线段AD、AP所围成图形的面积为y，y随x的变化而变化。在下列图象中，能正确反映y与x的函数关系的是（）

查看答案

题型：选择题

知识点：一次函数

复制

试题详情

纠错

难度：

使用次数：625

更新时间：2021-07-14

加入组卷

如图，P是y轴上一动点，是否存在平行于y轴的直线x＝t，使它与直线y＝x和直线分别交于点D、E（E在D的上方），且△PDE为等腰直角三角形。若存在，求t的值及点P的坐标；若不存在，请说明原因。

查看答案

题型：综合题

知识点：一次函数

复制

试题详情

纠错

难度：

使用次数：161

更新时间：2021-07-14

加入组卷

如图，某种旅行帽的帽沿接有两个塑料帽带，其中一个塑料帽带上有7个等距的小圆柱体扣，另一个帽带上扎有七个等距的扣眼，下表列出的是用第一扣分别去扣不同扣眼所测得帽圈直径的有关数据（单位：cm）：

扣眼号数（x）	1	2	3	4	5	6	7
帽圈直径（y）	22.92	22.60	22.28	21.96	21.64	21.32	21.00

（1）求帽圈直径y与扣眼号数x之间的一次函数关系式；

（2）小强的头围约为68.94cm，他将第一扣扣到第4号扣眼，你认为松紧合适吗？

查看答案

题型：解答题

知识点：一次函数

复制

试题详情

纠错

加入组卷

进入组卷

下载知识点

使用过本题的试卷：

2021-2022学年初中数学一次函数专题含解析

知识点：

一次函数

版权提示

该作品由: 用户刘敏分享上传

可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系可圈可点，我们核实后将及时进行处理。