如图，在△ABC

当前位置：

学科首页

九下第二十七章相似

相似三角形

试题详情

难度：

使用次数：235

更新时间：2022-03-27

纠错

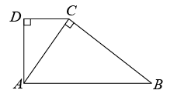
如图，在 △ ABC 和 △ ACD 中， AD ⊥ CD 于点 D ， AC ⊥ BC 于点 C ．请再添加一个条件，使，并加以证明．

查看答案

题型：解答题

知识点：相似三角形

下载试题

复制试题

【答案】

添加条件： AB // CD ，证明见解析（答案不唯一）

【解析】

【分析】

要证，通过观察发现两个三角形已经具备一组角相等，即，此时，可添加一组角相等即可．

【详解】

添加条件：．

证明： ∵ ，，

∴ ，

∵ ，

∴ ，

∴ ．

【点睛】

本题考查了相似三角形的判定，熟练掌握相似三角形的判定定理及正确找到对应角是解题的关键，此题是开放题，答案不唯一．

考点梳理:

根据可圈可点权威老师分析，试题“ ”主要考查你对相似三角形的判定等考点的理解。关于这些考点的“资料梳理”如下：

◎ 相似三角形的判定的定义

相似三角形：
对应角相等，对应边成比例的两个三角形叫做相似三角形。
互为相似形的三角形叫做相似三角形。

例如图中，若B'C'//BC，那么角B=角B'，角BAC=角B'A'C'，是对顶角，那么我们就说△ABC∽△AB'C'

◎ 相似三角形的判定的知识扩展

1、相似三角形：对应角相等，对应边成比例的两个三角形叫做相似三角形。
2、相似三角形的判定：
判定定理：（1）平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似。
（2）如果两个三角形的三组对应边的比相等，那么这两个三角形相似；
（3）如果两个三角形的两组对应边的比相等，并且相应的夹角相等，那么这两个三角形相似；
（4）如果一个三角形的两角与另一个三角形的两个角对应相等，那么这两个三角形相似。

◎ 相似三角形的判定的特性

相似三角形的判定：
1.基本判定定理
(1)平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似。
(2)如果一个三角形的两条边和另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似。(简叙为：两边对应成比例且夹角相等，两个三角形相似。)
(3)如果一个三角形的三条边与另一个三角形的三条边对应成比例，那么这两个三角形相似。(简叙为：三边对应成比例，两个三角形相似。)
(4)如果两个三角形的两个角分别对应相等（或三个角分别对应相等），那么这两个三角形相似。
2.直角三角形判定定理
(1)直角三角形被斜边上的高分成两个直角三角形和原三角形相似。
(2)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似。
3.一定相似：
（1）.两个全等的三角形
（全等三角形是特殊的相似三角形，相似比为1：1）
（2）.两个等腰三角形
（两个等腰三角形，如果其中的任意一个顶角或底角相等，那么这两个等腰三角形相似。）
（3）.两个等边三角形
(两个等边三角形，三个内角都是60度，且边边相等，所以相似)　
（4）.直角三角形中由斜边的高形成的三个三角形。

◎ 相似三角形的判定的知识点拨

相似三角形判定方法：
证两个相似三角形应该把表示对应顶点的字母写在对应的位置上。如果是文字语言的“△ABC与△DEF相似”，那么就说明这两个三角形的对应顶点可能没有写在对应的位置上，而如果是符号语言的“△ABC∽△DEF”，那么就说明这两个三角形的对应顶点写在了对应的位置上。
一、（预备定理）
平行于三角形一边的直线截其它两边所在的直线，截得的三角形与原三角形相似。（这是相似三角形判定的定理，是以下判定方法证明的基础。这个引理的证明方法需要平行线与线段成比例的证明）
二、如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
三、如果两个三角形的两组对应边成比例，并且相应的夹角相等,那么这两个三角形相似。
四、如果两个三角形的三组对应边成比例，那么这两个三角形相似
五（定义）
对应角相等，对应边成比例的两个三角形叫做相似三角形
六、两三角形三边对应垂直，则两三角形相似。
七、两个直角三角形中，斜边与直角边对应成比例，那么两三角形相似。
八、由角度比转化为线段比：h1/h2=Sabc

易失误
比值是一个具体的数字如：AB/EF=2
而比不是一个具体的数字如：AB/EF=2：1

◎ 相似三角形的判定的教学目标

1、经历三角形相似与全等的类比过程，进一步体验类比思想、特殊与一般的辩证思想。
2、通过经历两个三角形相似条件的探索过程，发现“两角对应相等的两个三角形相似”的判定方法；掌握判定两个三角形相似的基本方法。
3、进一步发展学生的探究、交流能力、合情推理能力和初步的逻辑推理意识，并能够运用三角形相似的条件解决简单问题。

◎ 相似三角形的判定的考试要求

能力要求：掌握
课时要求：120
考试频率：常考
分值比重：5

开通会员

登录并加入会员可无限制查看知识点解析

类题推荐：

相似三角形

难度：

使用次数：150

更新时间：2009-03-15

加入组卷

-如图，在平行四边形ABCD中，E是AD上一点，连结CE并延长交BA的延长线于点F，则下列结论中错误的是（）

A. ∠AEF＝∠DEC B. FA:CD＝AE:BC

C. FA:AB＝FE:EC D. AB＝DC

查看答案

题型：选择题

知识点：相似三角形

复制

试题详情

纠错

难度：

使用次数：182

更新时间：2021-07-13

加入组卷

在△ABC中，∠B＝25°，AD是BC边上的高，并且，则∠BCA的度数为____________。

查看答案

题型：填空题

知识点：相似三角形

复制

试题详情

纠错

难度：

使用次数：153

更新时间：2021-07-14

加入组卷

如图，在一个长40m、宽30m的长方形小操场上，王刚从A点出发，沿着A→B→C的路线以3m/s的速度跑向C地。当他出发4s后，张华有东西需要交给他，就从A地出发沿王刚走的路线追赶。当张华跑到距B地的D处时，他和王刚在阳光下的影子恰好重叠在同一条直线上。此时，A处一根电线杆在阳光下的影子也恰好落在对角线AC上。

（1）求他们的影子重叠时，两人相距多少米（DE的长）？

（2）求张华追赶王刚的速度是多少（精确到0.1m/s）？

查看答案

题型：解答题

知识点：相似三角形

复制

试题详情

纠错

难度：

使用次数：128

更新时间：2021-07-15

加入组卷

某市经济开发区建有B、C、D三个食品加工厂，这三个工厂和开发区A处的自来水厂正好在一个矩形的四个顶点上，它们之间有公路相通，且AB=CD=900米，AD=BC=1700米．自来水公司已经修好一条自来水主管道AN，BC两厂之间的公路与自来水管道交于E处，EC=500米．若自来水主管道到各工厂的自来水管道由各厂负担，每米造价800元．

（1）要使修建自来水管道的造价最低，这三个工厂的自来水管道路线应怎样设计？并在图形中画出；

（2）求出各厂所修建的自来水管道的最低的造价各是多少元？

查看答案

题型：解答题

知识点：相似三角形

复制

试题详情

纠错

难度：

使用次数：180

更新时间：2021-07-15

加入组卷

如图,AD是△ABC的角平分线, 延长AD交△ABC的外接圆O于点E,过C、D、E三点的圆O₁交AC的延长线于点F，连结EF、DF．

(1)求证：△AEF∽△FED；

(2) 若AD=6，DE=3, 求EF的长；

(3) 若DF∥BE, 试判断△ABE的形状，并说明理由．

查看答案

题型：综合题

知识点：相似三角形

复制

试题详情

纠错

加入组卷

进入组卷

下载知识点

使用过本题的试卷：

2021-2022学年初中图形的变化专题含解析

知识点：

相似三角形

版权提示

该作品由: 用户小小分享上传

可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系可圈可点，我们核实后将及时进行处理。