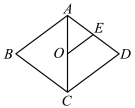
如图，在菱形 ABCD 中， O 、 E 分别是 AC 、 AD 的中点，连接 OE ，若 AB ＝ 10 ， AC ＝ 12 ，则 tan∠ AOE 的值为（　　）

A ． B ． C ． D ．

答案

D

【解析】

【分析】

连接 OD ，由菱形的性质可知 AD ＝ CD ＝ AB ＝ 10 ．由 O 是 AC 的中点结合等腰三角形 “ 三线合一 ” 得出 OD ⊥ AC ， OA ＝ OC =6 ．从而在 中，利用勾股定理可求出 OD 的长．由 O 、 E 分别是 AC 、 AD 的中点，即可根据三角形中位线的性质得出 OE ∥ CD ，从而得出 ∠ AOE ＝ ∠ ACD ，即求出 tan∠ ACD 即可．

【详解】

如图，连接 OD ，

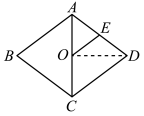
∵ 四边形 ABCD 为菱形，

∴ AD ＝ CD ＝ AB ＝ 10 ．

∵ O 是 AC 的中点，

∴ OD ⊥ AC ， OA ＝ OC AC ＝ 6 ，

由勾股定理得， OD ，

∵ O 、 E 分别是 AC 、 AD 的中点，

∴ OE 是 △ ACD 的中位线，

∴ OE ∥ CD ，

∴∠ AOE ＝ ∠ ACD ，

∴tan∠ AOE ＝ tan∠ ACD ，

故选： D ．

【点睛】

本题考查菱形的性质，等腰三角形 “ 三线合一 ” ，勾股定理，三角形中位线的性质以及求正切值．正确的作出辅助线是解题关键．