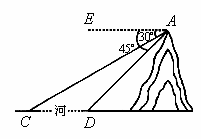
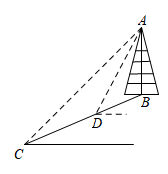
某通信公司准备逐步在歌乐山上建设 5 G 基站．如图，某处斜坡 CB 的坡度（或坡比）为 i ＝ 1∶2.4 ，通讯塔 AB 垂直于水平地面，在 C 处测得塔顶 A 的仰角为 45° ，在 D 处测得塔顶 A 的仰角为 53° ，斜坡路段 CD 长 26 米，则通讯塔 AB 的高度为（ ）（参考数据： ， ， ）

A ． 米 B ． 米 C ． 56 米 D ． 66 米

答案

B

【解析】

【分析】

通过作辅助线，利用斜坡 的坡度为 ， ，由勾股定理可求出 的长，设出 的长，根据坡度表示 ，进而表示出 ，由于 是等腰直角三角形，可表示 ，在 中由锐角三角函数可列方程求出 ，进而求出 ．

【详解】

解：如图，延长 与水平线交于 ，过 作 ， 为垂足，过 作 ， 为垂足，连接 ， ，

斜坡 的坡度为 ，

，

设 米，则 米，

在 中， 米，由勾股定理得，

，

即 ，

解得 ，

（米 ， （米 ，

斜坡 的坡度为 ，

设 米，则 米，

，

米，

米，

在 中， 米， 米，

，

，

解得 ，

（米 ， （米 ，

（米 ，

（米 ，

答：基站塔 的高为 米．

故选： B ．

【点睛】

本题考查解直角三角形 仰角俯角问题，坡度坡角问题，通过作垂线构造直角三角形，利用直角三角形的边角关系和坡度的意义进行计算是解题关键．