定义：把经过三角形的一个顶点并与其对边所在直线相切的圆叫做三角形的 “ 切接圆 ” ．根据上述定义解决下列问题，在 △ABC 中， AB=AC=5 ， BC=6 ，设 △ABC 的 “ 切接圆 ” 的半径为 r ．

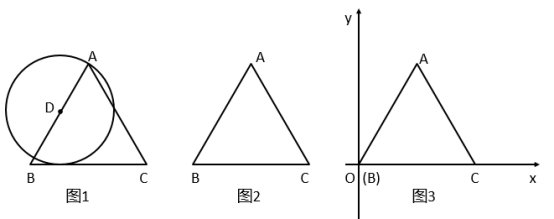
（ 1 ）如图 1 ， △ABC 的 “ 切接圆 ” 的圆心 D 在边 AB 上，求 r ；

（ 2 ）如图 2 ，请确定 r 的最小值，并说明理由；

（ 3 ）如图 3 ，把 △ABC 放在平面直角坐标系中，使点 B 与原点 O 重合，点 C 落在 x 轴正半轴上． 求证：以抛物线 上任意一点为圆心都可以作 △ABC 的 “ 切接圆 ” ．

答案

（ 1 ） ；（ 2 ） ；（ 3 ）证明过程见解析；

【分析】

（ 1 ）作 ， ，根据勾股定理和相似三角形的性质计算即可；

（ 2 ）判断出 r 的最小值范围，根据等面积法确定计算即可；

（ 3 ）设抛物线 上任意一点为 ，证明 P 到 x 轴的距离与 PA 的距离相等即可；

【详解】

（ 1 ）如图所示，作 ， ，

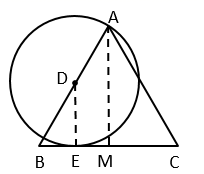
∵AM∥DE ， ， AB=AC ，

∴ ，

∴ ，

由题可知 ，

∴ ，

∴ ，

∴ ，

∴ ．

（ 2 ）由几何关系得，当这个图的直径是三角形的一条高时，最短；

∵A 到 BC 的距离为 4 ，

∴ ， ；

设 C 到 AB 的距离是 m ，

则 ，

∴ ，

∴ ， ，

∵ ＞ ，

∴ 为最小值，

∴ ；

（ 3 ）设抛物线 上任意一点为 ，因为抛物线的开口向上，顶点坐标为（ 3 ， 2 ），所以对于抛物线上任意一点来说，纵坐标均为正数，

则 P 到 x 轴的距离为 ，

① ，

∵ ，

∴ ，

∴ ，

将上式代入 ① 得，

，

∴ ，

即说明抛物线上任意一点 P 均是 △ABC 的切接圆圆心．

【点睛】

本题主要考查了与圆有关的计算，结合相似三角形的性质、勾股定理计算是解题的关键．