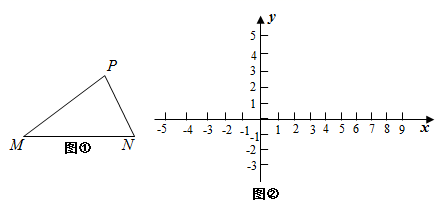
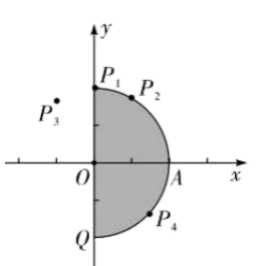
对于平面内的点 M 和点 N ，给出如下定义：点 P 为平面内的一点，若点 P 使得 △ PMN 是以 ∠ M 为顶角且 ∠ M 小于 90° 的等腰三角形，则称点 P 是点 M 关于点 N 的锐角等腰点．如图 ① ，点 P 是点 M 关于点 N 的锐角等腰点．

在平面直角坐标系 xOy 中，点 O 是坐标原点．

（ 1 ）已知点 A (2 ， 0) ，在点 中，是点 O 关于点 A 的锐角等腰点的是 ；

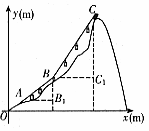
（ 2 ）已知点 B (3 ， 0) ，点 C 在直线 y ＝ 2 x ＋ b 上，若点 C 是点 O 关于点 B 的锐角等腰点，求实数 b 的取值范围；

（ 3 ）点 D 是 x 轴上的动点， D ( t ， 0) ， E ( t ﹣ 2 ， 0) ，点 F ( m ， n ) 是以 D 为圆心， 2 为半径的圆上一个动点，且满足 n ≥0 ．直线 y ＝﹣ 2 x ＋ 4 与 x 轴和 y 轴分别交于点 H ， K ，若线段 HK 上存在点 E 关于点 F 的锐角等腰点，请直接写出 t 的取值范围．

答案

（ 1 ） P ₂ ； P ₄ ；（ 2 ） ；（ 3 ）

【分析】

（ 1 ）由新定义可得点 关于点 的锐角等腰点在半圆 上，从而可得答案；

（ 2 ）如图，当直线 过点 时， 当直线 与半圆 切于点 与 轴交于点 与 轴交于点 时，求解 的值即可得到答案；

（ 3 ）由题意可得：点 关于点 的锐角等腰点在半圆 上，点 在半圆 上，点 在半圆 上，（将半圆 绕点 旋转），如图 ① ．半圆 扫过的区域为图 ② 中的阴影部分，再分情况构建直线与阴影部分相切，分别求解此时 的值，从而可得答案．

【详解】

解：（ 1 ）如图，点 关于点 的锐角等腰点在半圆 上（不包括 三点），

由

＜

所以点 满足条件．

（ 2 ）如图，当直线 过点 时，

当直线 与半圆 切于点 与 轴交于点 与 轴交于点 时，

令 则

＜

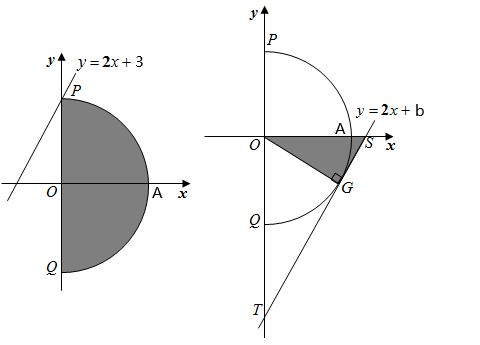
所以点 C 是点 O 关于点 B 的锐角等腰点时，实数 b 的取值范围为 ＜ ．

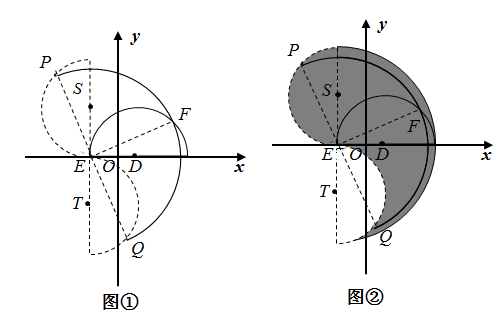
（ 3 ）由题意可得：点 关于点 的锐角等腰点在半圆 上，

点 在半圆 上，点 在半圆 上，（将半圆 绕点 旋转），如图 ① ．

半圆 扫过的区域为图 ② 中的阴影部分，

如图 ③ ，阴影部分与 切于点

同理可得：

则 即

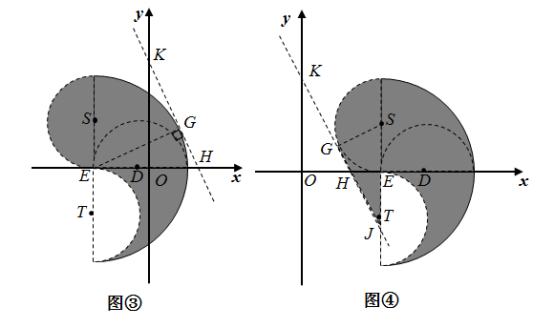
如图 ④ ，阴影部分与 切于点 则

则

则

即

则

t 的取值范围为： ＜

【点睛】

本题考查的是新定义情境下的函数与几何的综合应用，考查了锐角三角函数的应用，切线的性质定理，弄懂题意构建符合题意的图形是解题的关键．