如图，在 △ ABC 中， AB ＝ 3 ， AC ＝ 4 ， BC ＝ 5 ．在同一平面内， △ ABC 内部一点 O 到 AB ， AC ， BC 的距离都等于 a （ a 为常数），到点 O 的距离等于 a 的所有点组成图形 G ．

（ 1 ）直接写出 a 的值；

（ 2 ）连接 BO 并延长，交 AC 于点 M ，过点 M 作 MN ⊥ BC 于点 N ．

① 求证： ∠ BMA ＝ ∠ BMN ；

② 求直线 MN 与图形 G 的公共点个数．

答案

（ 1 ） 1 ；（ 2 ） ① 见解析； ②1 个

【分析】

（ 1 ）根据题意可得三角形 ABC 是直角三角形，再根据切线长定理即可求出 a 的值；

（ 2 ） ① 根据题意可得点 O 是三角形 ABC 的内心，再根据三角形内角和即可得结论；

② 作 OE ⊥ MN 于点 E ，根据角平分线的性质可得 OD = OE ，所以得 OE 为圆 O 的半径，进而可得 MN 为圆 O 的切线，即可得出结论．

【详解】

解：（ 1 ）如图，

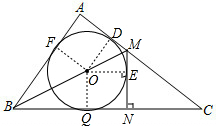
∵ AB =3 ， AC =4 ， BC =5 ，

∴ AB ² + AC ² = BC ² ，

∴∠ A =90° ，

∴△ ABC 是直角三角形，

由题意可知：图形 G 是以 O 为圆心， a 为半径的圆， AB ， AC ， BC 与圆 O 相切，

设切点分别为 F ， D ， Q ，连接 OF ， OD ， OQ ，

∴ OF ⊥ AB ， OD ⊥ AC ， OQ ⊥ BC ，

∴ 四边形 AFOD 为正方形，

∴ AF = AD = OF = OD = a ，

根据切线长定理可知： BF = BQ =3- a ， CD = CQ =4- a ，

∴3- a +4- a =5 ，解得 a =1 ；

（ 2 ） ① 由题意可知：点 O 是 △ ABC 的内心，

∴∠ ABM =∠ CBM ，

∵ MA ⊥ AB ， MB ⊥ BC ，

∴∠ A =∠ BNM =90° ，

∴∠ BMA =∠ BMN ；

② 如图，作 OE ⊥ MN 于点 E ，

∵∠ BMA =∠ BMN ， OD ⊥ AC ，

∴ OD = OE ，

∴ OE 为圆 O 的半径，

∴ MN 为圆 O 的切线，

∴ 直线 MN 与图形 G 的公共点个数为 1 ．

【点睛】

本题考查了三角形的内切圆与内心，解决本题的关键是掌握三角形的内心定义．