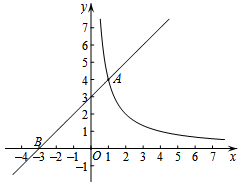
如图，在平面直角坐标系 xOy 中，直线 y ＝ x ＋ 3 与函数 y ＝ （ x ＞ 0 ）的图象交于点 A (1 ， m ) ，与 x 轴交于点 B ．

（ 1 ）求 m ， k 的值；

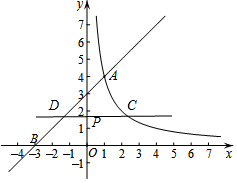
（ 2 ）过动点 P (0 ， n ) （ n ＞ 0 ）作平行于 x 轴的直线，交函数 y ＝ （ x ＞ 0 ）的图象于点 C ，交直线 y ＝ x ＋ 3 于点 D ．

① 当 n ＝ 2 时，求线段 CD 的长；

② 若 CD ≥ OB ，结合函数的图象，直接写出 n 的取值范围．

答案

（ 1 ） m =4 ， k =4 ；（ 2 ） ①3 ； ②0 ＜ n ≤2 或 ．

【分析】

（ 1 ）先利用一次函数解析式求出 m 的值，即可得到 A 点坐标，然后将 A 点坐标代入反比例函数解析式即可求得 k 的值；

（ 2 ） ① 先确定 C 点和 D 点的横坐标，然后求两横坐标之差即可解答；

② 先确定 B 点坐标为（ -3 ， 0 ），再根据 C 、 D 的纵坐标都为 n ，然后再根据题意确定 C 、 D 的坐标，最后分点 C 在点 D 的右侧和点 C 在点 D 的左侧两种情况解答即可．

【详解】

解： ∵ 直线 y = x +3 经过点 A （ 1 ， m ），

∴ m =1+3=4

∴ 反比例函数 y ＝ 的图象经过点 A （ 1 ， 4 ），

∴ k =1×4=4 ；

（ 2 ）如图： ① 当 n =2 时，点 P 的坐标为（ 0 ， 2 ） .

当 y =2 时， 2= ，解得 x =2 ，即点 C 的坐标为（ 2 ， 2 ）

当 y =2 时， x +3=2 ，解得 x =-1 ，即点 D 的坐标为（ -1 ， 2 ）

∴ CD =2- （ -1 ） =3 ；

② 如图：当 y =0 时， x +3=0 ，解得 x =-3 ，则 B （ -3 ， 0 ）

当 y = n 时， n = ，解得 x = ，即点 C 的坐标为（ ， n ） .

当 y = n 时， x +3= n ，解得 x = n -3 ，即点 D 的坐标为（ n -3 ， n ）

当点 C 在点 D 的右侧时，

∵ CD = OB

∴ - （ n -3 ） =3 ，解得 n ₁ =2 ， n ₂ =-2 （舍去）

∴ 当 0< n ≤2 时， CD ≥ OB ；

当点 C 在点 D 的左侧时

∵ CD = OB ，即 n -3- =3 ，解得 （舍去）

∴ 当 n ≥ 时， CD ≥ OB ；

综上所述， n 的取值范围为 0 ＜ n ≤2 或 ．

【点睛】

本题主要考查了反比例函数与一次函数图像的交点问题以及运用待定系数法求函数解析式等知识点，掌握数形结合思想成为解答本题的关键．