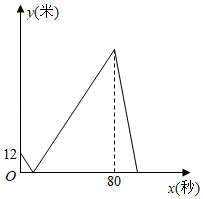
甲、乙两人在一条长 400 米的直线跑道上同起点、同终点、同方向匀速跑步，先到终点的人原地休息．已知甲先出发 3 秒，在跑步过程中甲、乙两人之间的距离 ( 米 ) 与乙出发的时间 x ( 秒 ) 之间的函数关系如图所示，正确的个数为（    ）

① 乙的速度为 5 米 / 秒；

② 离开起点后，甲、乙两人第一次相遇时，距离起点 12 米；

③ 甲、乙两人之间的距离超过 32 米的时间范围是 ；

④ 乙到达终点时，甲距离终点还有 68 米．

A ． 4 B ． 3 C ． 2 D ． 1

答案

B

【分析】

利用乙用 80 秒跑完 400 米求速度可判断 ① ；利用甲先走 3 秒和 12 米求出甲速度，根据乙追甲相差 12 米求时间 =12 秒再求距起点的距离可判断 ② ；利用两人间距离列不等式 5 （ t-12 ） -4(t-12) 32 ，和乙到终点，甲距终点列不等式 4 t +12 400-32 解不等式可判断 ③ ；

根据乙到达终点时间，求甲距终点距离可判断 ④ 即可

【详解】

解： ①∵ 乙用 80 秒跑完 400 米

∴ 乙的速度为 =5 米 / 秒；

故 ① 正确；

②∵ 乙出发时，甲先走 12 米，用 3 秒钟，

∴ 甲的速度为 米 / 秒，

∴ 乙追上甲所用时间为 t 秒，

5 t -4 t =12 ，

∴ t =12 秒，

∴12×5=60 米，

∴ 离开起点后，甲、乙两人第一次相遇时，距离起点 60 米；

故 ② 不正确；

③ 甲乙两人之间的距离超过 32 米设时间为 t 秒，

∴5 （ t-12 ） -4(t-12) 32 ，

∴t 44 ，

当乙到达终点停止运动后，

4 t +12 400-32 ，

∴t 89 ，

甲、乙两人之间的距离超过 32 米的时间范围是 ；

故 ③ 正确；

④ 乙到达终点时，

甲距终点距离为： 400-12-4×80=400-332=68 米，

甲距离终点还有 68 米．

故 ④ 正确；

正确的个数为 3 个．

故选择 B ．

【点睛】

本题考查一次函数的图像应用问题，仔细阅读题目，认真观察图像，从图像中获取信息，掌握一次函数的图像应用，列不等式与解不等式，关键是抓住图像纵轴是表示两人之间的距离，横坐标表示乙出发时间，拐点的意义是解题关键．