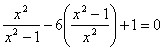已知 和 均是以 为自变量的函数，当 时，函数值分别为 和 ，若存在实数 ，使得 ，则称函数 和 具有性质 ．以下函数 和 具有性质 的是（ ）

A ． 和

B ． 和

C ． 和

D ． 和

答案

A

【分析】

根据题中所给定义及一元二次方程根的判别式可直接进行排除选项．

【详解】

解：当 时，函数值分别为 和 ，若存在实数 ，使得 ，

对于 A 选项则有 ，由一元二次方程根的判别式可得： ，所以存在实数 m ，故符合题意；

对于 B 选项则有 ，由一元二次方程根的判别式可得： ，所以不存在实数 m ，故不符合题意；

对于 C 选项则有 ，化简得： ，由一元二次方程根的判别式可得： ，所以不存在实数 m ，故不符合题意；

对于 D 选项则有 ，化简得： ，由一元二次方程根的判别式可得： ，所以不存在实数 m ，故不符合题意；

故选 A ．

【点睛】

本题主要考查一元二次方程根的判别式、二次函数与反比例函数的性质，熟练掌握一元二次方程根的判别式、二次函数与反比例函数的性质是解题的关键．