如图，设点是直线外一

当前位置：

学科首页

七下第五章相交线与平行线

相交线

试题详情

难度：

使用次数：102

更新时间：2021-06-30

纠错

如图，设点是直线外一点，，垂足为点，点是直线上的一个动点，连接，则（）

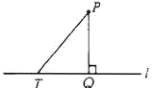
A ． B ． C ． D ．

查看答案

题型：选择题

知识点：相交线

下载试题

复制试题

【答案】

【分析】

根据垂线段距离最短可以判断得出答案．

【详解】

解：根据点是直线外一点，，垂足为点，

是垂线段，即连接直线外的点与直线上各点的所有线段中距离最短，

当点与点重合时有，

综上所述：，

故选： C ．

【点睛】

本题考查了垂线段最短的定义，解题的关键是：理解垂线段最短的定义．

考点梳理:

根据可圈可点权威老师分析，试题“ ”主要考查你对相交线等考点的理解。关于这些考点的“资料梳理”如下：

◎ 相交线的定义

相交线：
当两条不同的直线有一个公共点时，就称这两条直线相交，这个公共点叫做它们的交点。

◎ 相交线的知识扩展

相交线：当两条不同的直线有一个公共点时，就称这两条直线相交，这个公共点叫做它们的交点。

◎ 相交线的特性

相交线性质：

∠1和∠2有一条公共边OC，它们的另一边互为反向延长线(∠1和∠2互补)，具有这种关系的两个角，互为邻补角。
∠1和∠3有一个公共顶点O，并且∠1的两边分别是∠3的两边的反向延长线，具有这种位置关系的两个角，互为对顶角。
∠1与∠2互补，∠3与∠2互补，由“同角的补角相等”，可以得出∠1=∠3.类似地,∠2=∠4.这样，
我们得到了对顶角的性质：对顶角相等。

◎ 相交线的知识对比

垂线：
垂直是相交的一种特殊情形，两条直线互相垂直，其中的一条直线叫做另一条直线的垂线，它们的交点叫做垂足。
经过一点（已知直线上或直线外）,能画出已知直线的一条垂线,并且只能画出一条垂线,即:
过一点有且只有一条直线与已知直线垂直。
连接直线外一点与直线上各点的所有线段中,垂线段最短.
简单说成:垂线段最短。
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。

◎ 相交线的教学目标

1、理解邻补角、对顶角的概念。
2、能从图中辨认邻补角与对顶角，能画图表示邻补角、对顶角。
3、掌握平面内两条直线相交时，所形成的邻补角、对顶角的数量关系，能通过简单推理得到“对顶角相等”的性质，并能运用它进行简单计算和推理。
4、进一步提高识图能力，初步渗透推理论证的思想及书写格式，感受数学的严谨。

◎ 相交线的考试要求

能力要求：了解
课时要求：30
考试频率：少考
分值比重：2

开通会员

登录并加入会员可无限制查看知识点解析

类题推荐：

相交线

难度：

使用次数：472

更新时间：2009-03-15

加入组卷

已知∠1与∠2是对顶角,∠1与∠3是邻补角,则∠2+∠3=_______.

查看答案

题型：填空题

知识点：相交线

复制

试题详情

纠错

难度：

使用次数：105

更新时间：2009-03-15

加入组卷

已知直线a∥b,点M到直线a的距离是5cm,到直线b的距离是3cm,那么直线a和直线b之间的距离为_______.

查看答案

题型：填空题

知识点：相交线

复制

试题详情

纠错

难度：

使用次数：255

更新时间：2009-03-15

加入组卷

如图，∠ADE和∠CED是 ( )

A．同位角 B．内错角 C．同旁内角 D．互为补角

查看答案

题型：选择题

知识点：相交线

复制

试题详情

纠错

难度：

使用次数：626

更新时间：2009-03-15

加入组卷

如下图，直线，相交于点O，若∠1等于40°，则∠2等于（）

A．50° B．60° C．140° D．160°

查看答案

题型：选择题

知识点：相交线

复制

试题详情

纠错

难度：

使用次数：74

更新时间：2009-03-15

加入组卷

如图所示，一根长2a的木棍(船)，斜靠在与地面(OM)垂直的墙(ON)上，设木棍的中点为P，若木棍A端沿墙下滑，且B端沿地面向右滑行．

(1)请判断木棍滑动的过程中，点P到点O的距离是否变化，并简述理由．

(2)在木棍滑动的过程中，当滑动到什么位置时，△AOB的面积最大？

查看答案

题型：作图题

知识点：相交线

复制

试题详情

纠错

加入组卷

进入组卷

下载知识点

使用过本题的试卷：

2021年浙江省杭州市中考数学真题含详解

知识点：

相交线

版权提示

该作品由: 用户刘利超分享上传

可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系可圈可点，我们核实后将及时进行处理。