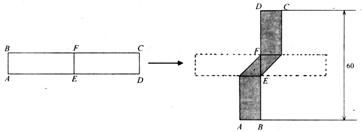
在几何体表面上，蚂蚁怎样爬行路径最短？

（ 1 ）如图 ① ，圆锥的母线长为 ， B 为母线 的中点，点 A 在底面圆周上， 的长为 ．在图 ② 所示的圆锥的侧面展开图中画出蚂蚁从点 A 爬行到点 B 的最短路径，并标出它的长（结果保留根号）．

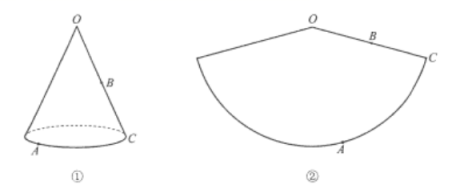
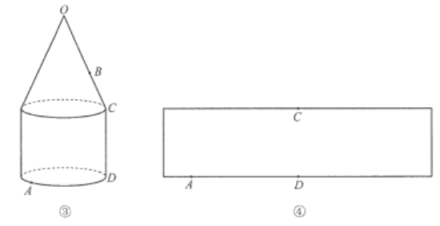
（ 2 ）图 ③ 中的几何体由底面半径相同的圆锥和圆柱组成． O 是圆锥的顶点，点 A 在圆柱的底面圆周上．设圆锥的母线长为 l ，圆柱的高为 h ．

① 蚂蚁从点 A 爬行到点 O 的最短路径的长为 ________ （用含 l ， h 的代数式表示）．

② 设 的长为 a ，点 B 在母线 上， ．圆柱的侧面展开图如图 ④ 所示，在图中画出蚂蚁从点 A 爬行到点 B 的最短路径的示意图，并写出求最短路径的长的思路．

答案

（ 1 ）作图如图所示；（ 2 ） ① h + l ； ② 见解析．

【分析】

（ 1 ）根据两点之间线段最短，即可得到最短路径；连接 OA ， AC ，可以利用弧长与母线长求出 ∠ AOC ，进而证明出 △ OAC 是等边三角形，利用三角函数即可求解；

（ 2 ） ① 由于圆锥底面圆周上的任意一点到圆锥顶点的距离都等于母线长，因此只要蚂蚁从点 A 爬到圆锥底面圆周上的路径最短即可，因此顺着圆柱侧面的高爬行，所以得出最短路径长即为圆柱的高 h 加上圆锥的母线长 l ；

② 如图，根据已知条件，设出线段 GC 的长后，即可用它分别表示出 OE 、 BE 、 GE 、 AF ，进一步可以表示出 BG 、 GA ，根据 B 、 G 、 A 三点共线，在 Rt △ ABH 中利用勾股定理建立方程即可求出 GC 的长，最后依次代入前面线段表达式中即可求出最短路径长．

【详解】

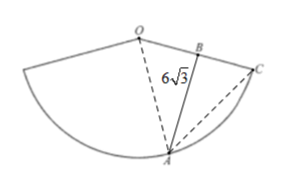
解：（ 1 ）如图所示，线段 AB 即为蚂蚁从点 A 爬行到点 B 的最短路径；

设 ∠ AOC = n ° ，

∵ 圆锥的母线长为 ， 的长为 ，

∴ ，

∴ ；

连接 OA 、 CA ，

∵ ，

∴ 是等边三角形，

∵ B 为母线 的中点，

∴ ，

∴ ．

（ 2 ） ① 蚂蚁从点 A 爬行到点 O 的最短路径为：先沿着过 A 点且垂直于地面的直线爬到圆柱的上底面圆周上，再沿圆锥母线爬到顶点 O 上，因此，最短路径长为 h + l

② 蚂蚁从点 A 爬行到点 B 的最短路径的示意图如下图所示，线段 AB 即为其最短路径（ G 点为蚂蚁在圆柱上底面圆周上经过的点，图中两个 C 点为图形展开前图中的 C 点）；

求最短路径的长的思路如下：如图，连接 OG ，并过 G 点作 GF ⊥ AD ，垂足为 F ，由题可知， ， GF = h ， OB = b ，

由 的长为 a ，得展开后的线段 AD = a ，设线段 GC 的长为 x ，则 的弧长也为 x ，由母线长为 l ，可求出 ∠COG ，

作 BE ⊥ OG ，垂足为 E ，

因为 OB = b ，可由三角函数求出 OE 和 BE ，从而得到 GE ，利用勾股定理表示出 BG ，

接着由 FD = CG = x ，得到 AF = a - x ，利用勾股定理可以求出 AG ，

将 AF + BE 即得到 AH ，将 EG + GF 即得到 HB ，

因为两点之间线段最短， ∴ A 、 G 、 B 三点共线，

利用勾股定理可以得到： , 进而得到关于 x 的方程，即可解出 x ，

将 x 的值回代到 BG 和 AG 中，求出它们的和即可得到最短路径的长．

【点睛】

本题考查的是曲面上的最短路径问题，涉及到圆锥和圆柱以及它们的组合体上的最短路径问题，解题过程涉及到 “ 两点之间、线段最短 ” 以及勾股定理和三角函数等知识，本题为开放性试题，答案形式不唯一，对学生的空间想象能力以及图形的感知力要求较高，蕴含了数形结合等思想方法．