如图， ∠ AOB=60° ，点 P 是 ∠ AOB 内的定点且 OP= ，若点 M、N 分别是射线 OA、OB 上异于点 O 的动点，则 △ PMN 周长的最小值是（　　）

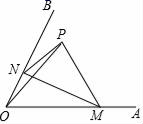
A ． B ． C ． 6 D ． 3

答案

D

【解析】

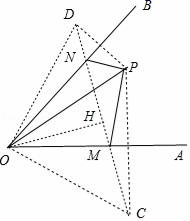
分析：作 P 点分别关于 OA、OB 的对称点 C、D ，连接 CD 分别交 OA、OB 于 M、N ，如图，利用轴对称的性质得 MP=MC，NP=ND，OP=OD=OC= ， ∠ BOP= ∠ BOD， ∠ AOP= ∠ AOC ，所以 ∠ COD=2 ∠ AOB=120° ，利用两点之间线段最短判断此时 △ PMN 周长最小，作 OH ⊥ CD 于 H ，则 CH=DH ，然后利用含 30 度的直角三角形三边的关系计算出 CD 即可．

详解：作 P 点分别关于 OA、OB 的对称点 C、D ，连接 CD 分别交 OA、OB 于 M、N ，如图，

则 MP=MC，NP=ND，OP=OD=OC= ， ∠ BOP= ∠ BOD， ∠ AOP= ∠ AOC，

∴ PN+PM+MN=ND+MN+MC=DC， ∠ COD= ∠ BOP+ ∠ BOD+ ∠ AOP+ ∠ AOC=2 ∠ AOB=120°，

∴此时 △ PMN 周长最小，

作 OH ⊥ CD 于 H ，则 CH=DH，

∵∠ OCH=30°，

∴ OH= OC= ，

CH= OH= ,

∴ CD=2CH=3．

故选 D．

点睛：本题考查了轴对称﹣最短路线问题：熟练掌握轴对称的性质，会利用两点之间线段最短解决路径最短问题．