如图， ∠1=100°，∠2=145° ，那么 ∠3=(    ).

A ． 55° B ． 65° C ． 75° D ． 85°

答案

B

【解析】

试题解析：

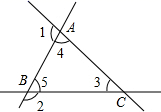
∵∠1=100°，∠2=145°，

∴∠4=180°-∠1=180°-100°=80°，

∠5=180°-∠2=180°-145°=35°，

∵∠3=180°-∠4-∠5，

∴∠3=180°-80°-35°=65°．

故选 B．