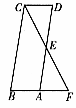
如图，在矩形ABCD中，E是AB边的中点，沿EC对折矩形ABCD，使B点落在点P处，折痕为EC，连结AP并延长AP交CD于F点，连结CP并延长CP交AD于Q点．给出以下结论：

①四边形AECF为平行四边形；

②∠PBA=∠APQ；

③△FPC为等腰三角形；

④△APB≌△EPC；

其中正确结论的个数为（　　）

A．1                           B．2                           C．3                           D．4

答案

B

【解析】

分析：①根据三角形内角和为180°易证∠PAB+∠PBA=90°，易证四边形AECF是平行四边形，即可解题；

②根据平角定义得：∠APQ+∠BPC=90°，由正方形可知每个内角都是直角，再由同角的余角相等，即可解题；

③根据平行线和翻折的性质得：∠FPC=∠PCE=∠BCE，∠FPC≠∠FCP，且∠PFC是钝角，△FPC不一定为等腰三角形；

④当BP=AD或△BPC是等边三角形时，△APB≌△FDA，即可解题．

详解：①如图，EC，BP交于点G；

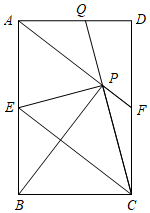
∵点P是点B关于直线EC的对称点，

∴EC垂直平分BP，

∴EP=EB，

∴∠EBP=∠EPB，

∵点E为AB中点，

∴AE=EB，

∴AE=EP，

∴∠PAB=∠PBA，

∵∠PAB+∠PBA+∠APB=180°，即∠PAB+∠PBA+∠APE+∠BPE=2（∠PAB+∠PBA）=180°，

∴∠PAB+∠PBA=90°，

∴AP⊥BP，

∴AF∥EC；

∵AE∥CF，

∴四边形AECF是平行四边形，

故①正确；

②∵∠APB=90°，

∴∠APQ+∠BPC=90°，

由折叠得：BC=PC，

∴∠BPC=∠PBC，

∵四边形ABCD是正方形，

∴∠ABC=∠ABP+∠PBC=90°，

∴∠ABP=∠APQ，

故②正确；

③∵AF∥EC，

∴∠FPC=∠PCE=∠BCE，

∵∠PFC是钝角，

当△BPC是等边三角形，即∠BCE=30°时，才有∠FPC=∠FCP，

如右图，△PCF不一定是等腰三角形，

故③不正确；

④∵AF=EC，AD=BC=PC，∠ADF=∠EPC=90°，

∴Rt△EPC≌△FDA（HL），

∵∠ADF=∠APB=90°，∠FAD=∠ABP，

当BP=AD或△BPC是等边三角形时，△APB≌△FDA，

∴△APB≌△EPC，

故④不正确；

其中正确结论有①②，2个，

故选B．

点睛：本题考查了全等三角形的判定和性质，等腰三角形的性质和判定，矩形的性质，翻折变换，平行四边形的判定，熟练掌握全等三角形的判定与性质是解本题的关键．