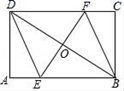
如图,在矩形ABCD中,BD的垂直平分线分别交AB、CD、BD于E、F、O,连接DE、BF.
(1)求证:四边形BEDF是菱形;
(2)若AB=8cm,BC=4cm,求四边形DEBF的面积.
答案
(1)证明见解析;(2)20cm2.
【解析】
(1)先证明△BOE≌△DOF,得出EO=FO,且OB=OD,再根据EF垂直平分BD,可得出四边形BEDF为菱形;
(2) 由菱形的性质知BE=DE,在Rt△ADE中,根据DE2=AE2+DA2列式求解即可.
【详解】
证明:(1)∵四边形ABCD是矩形,O是BD的中点,
∴∠A=90°,AD=BC=4,AB∥DC,OB=OD,
∴∠OBE=∠ODF
在△BOE和△DOF中,
∴△BOE≌△DOF(ASA),
∴EO=FO,且OB=OD
∴四边形BEDF是平行四边形,
∵EF垂直平分BD
∴BE=DE
∴四边形BEDF是菱形
(2)∵四边形BEDF是菱形
∴BE=DE,
在Rt△ADE中,DE2=AE2+DA2,
∴BE2=(8﹣BE)2+16,
∴BE=5
∴四边形DEBF的面积=BE×AD=20cm2.
【点睛】
本题考查了菱形的判定与性质、线段垂直平分线的性质、勾股定理、矩形的性质以及面积的求法等知识,熟练掌握菱形的判定与性质是解答本题的关键.

 。
。