初中数学2021年初专题周练——勾股定理训练题（一）【含详解】
初中
整体难度：偏难
2021-01-13
题号
一
二
三
四
五
评分
一、选择题 (共40题)
添加该题型下试题
1.
已知直角三角形两边的长为3和4，则此三角形的周长为（ ）
A．12 B．7+
C．12或7+ D．以上都不对
难度：
知识点：勾股定理
使用次数：267
【答案】
C
【详解】
设Rt△ABC的第三边长为x，①当4为直角三角形的直角边时，x为斜边，由勾股定理得，x=
=5，此时这个三角形的周长=3+4+5=12；②当4为直角三角形的斜边时，x为直角边，由勾股定理得，x=
，此时这个三角形的周长=3+4+
=7+．故选C
2.
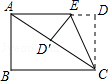
如图，将长方形纸片ABCD折叠，使边DC落在对角线AC上，折痕为CE，且D点落在对角线D′处．若AB=3，AD=4，则ED的长为
A．
B．3 C．1 D．
难度：
知识点：勾股定理
使用次数：244
【答案】
A
【分析】
首先利用勾股定理计算出AC的长，再根据折叠可得△DEC≌△D′EC，设ED=x，则D′E=x，AD′=AC﹣CD′=2，AE=4﹣x，再根据勾股定理可得方程22+x2=（4﹣x）2，再解方程即可
【详解】
∵AB=3，AD=4，∴DC=3
∴根据勾股定理得AC=5
根据折叠可得：△DEC≌△D′EC，
∴D′C=DC=3，DE=D′E
设ED=x，则D′E=x，AD′=AC﹣CD′=2，AE=4﹣x，
在Rt△AED′中：（AD′）2+（ED′）2=AE2，即22+x2=（4﹣x）2，
解得：x=
故选A.
3.
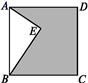
如图,已知点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )
A．48 B．60
C．76 D．80
难度：
知识点：勾股定理
使用次数：198
【答案】
C
【解析】
试题解析：∵∠AEB=90°，AE=6，BE=8，
∴AB=
∴S阴影部分=S正方形ABCD-SRt△ABE=102-
=100-24
=76.
故选C.
考点：勾股定理.
4.
如图所示，圆柱的高AB=3，底面直径BC=3，现在有一只蚂蚁想要从A处沿圆柱表面爬到对角C处捕食，则它爬行的最短距离是（ ）
A．
B．
C．
D．
难度：
知识点：勾股定理
使用次数：206
【答案】
C
【解析】
分析：要求最短路径，首先要把圆柱的侧面展开，利用两点之间线段最短，然后利用勾股定理即可求解．
详解：把圆柱侧面展开，展开图如图所示，点A、C的最短距离为线段AC的长．
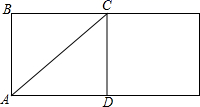
在Rt△ADC中，∠ADC=90°，CD=AB=3，AD为底面半圆弧长，AD=1.5π，
所以AC=
，
故选C．
点睛：本题考查了平面展开-最短路径问题，解题的关键是会将圆柱的侧面展开，并利用勾股定理解答．
5.
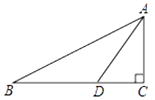
如图,在
中,
,
,点
在
上,
,
,则的长为（ ）
A．
B．
C．
D．
难度：
知识点：勾股定理
使用次数：124
【答案】
B
【分析】
根据
，可得∠B=∠DAB，即
，在Rt△ADC中根据勾股定理可得DC=1，则BC=BD+DC=
.
【详解】
解：∵∠ADC为三角形ABD外角
∴∠ADC=∠B+∠DAB
∵
∴∠B=∠DAB
∴
在Rt△ADC中，由勾股定理得：
∴BC=BD+DC=
故选B
【点睛】
本题考查勾股定理的应用以及等角对等边，关键抓住这个特殊条件.
本卷还有95题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
100
总体难度：
偏难
难度统计
难度系数
数量
占比
中等
59
59.0%
偏难
28
28.00%
容易
6
6.0%
基础
3
3.0%
很难
4
4.0%
题型统计
大题类型
数量
占比
选择题
40
40.0%
填空题
25
25.0%
解答题
35
35.0%
知识点统计
知识点
数量
占比
勾股定理
63
63.0%
全等三角形
3
3.0%
勾股定理的逆定理
6
6.0%
等腰三角形
6
6.0%
课题学习 最短路径问题
2
2.0%
平面直角坐标系
3
3.0%
实数
1
1.0%
角的平分线的性质
2
2.0%
三角形全等的判定
8
8.0%
勾股定理单元测试
2
2.0%
直射、射线、线段
1
1.0%
解一元二次方程
1
1.0%
一次函数
1
1.0%
一元二次方程
1
1.0%
版权提示
该作品由: 用户李超分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。