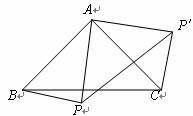
(1)问题发现:如图1,△ABC与△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,则线段AE、BD的数量关系为_______,AE、BD所在直线的位置关系为________;
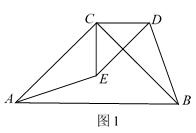
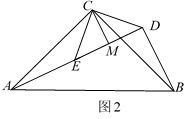
(2)深入探究:在(1)的条件下,若点A,E,D在同一直线上,CM为△DCE中DE边上的高,请判断∠ADB的度数及线段CM,AD,BD之间的数量关系,并说明理由;
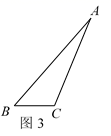
(3)解决问题:如图3,已知△ABC中,AB=7,BC=3,∠ABC=45°,以AC为直角边作等腰直角△ACD,∠CAD=90°,AC=AD,连接BD,则![]() 的长为 .
的长为 .
答案
(1)相等,垂直;(2)AD=2CM+BD;(3)![]() 或7
或7![]() ﹣3
﹣3
【分析】
(1)结论:AE=BD,AE⊥BD.如图1中,延长AE交BD于点H,AH交BC于点O.只要证明△ACE≌△BCD(SAS),即可解决问题;
(2)结论:AD=2CM+BD,只要证明△ACE≌△BCD(SAS),即可解决问题;
(3)分两种情形分别画出图形,构造全等三角形解决问题即可;
【详解】
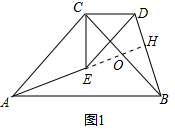
(1)结论:AE=BD,AE⊥BD.
理由:如图1中,延长AE交BD于点H,AH交BC于点O.
∵△ACB和△DCE均为等腰直角三角形,
∠ACB=∠DCE=90°,
∴AC=BC,CD=CE,
∴∠ACE=∠BCD,
∴△ACE≌△BCD(SAS),
∴AE=BD,∠CAE=∠CBD,
∵∠CAE+∠AOC=90°,∠AOC=∠BOH,
∴∠BOH+∠CBD=90°
∴∠AHB=90°,
∴AE⊥BD.
故答案是:AE=BD,AE⊥BD.
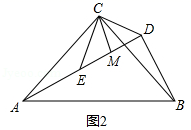
(2)结论:AD=2CM+BD,
理由:如图2中,
∵△ACB和△DCE均为等腰直角三角形,
∠ACB=∠DCE=90°,
∴AC=BC,CD=CE,
∴∠ACE=∠BCD,
∴△ACE≌△BCD(SAS),
∴AE=BD,∠BDC=∠AEC=135°.
∴∠ADB=∠BDC﹣∠CDE=135°﹣45°=90°;
在等腰直角三角形DCE中,CM为斜边DE上的高,
∴CM=DM=ME,
∴DE=2CM.
∴AD=DE+AE=2CM+BD.
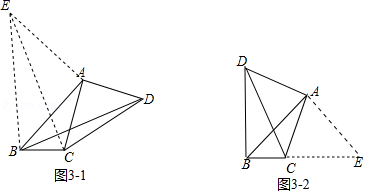
(3)情形1:如图3﹣1中,在△ABC的外部,以A为直角顶点作等腰直角△BAE,使∠BAE=90°,AE=AB,连接EA、EB、EC.
∵∠ACD=∠ADC=45°,
∴AC=AD,∠CAD=90°,
∴∠BAE+∠BAC=∠CAD+∠BAC,即∠EAC=∠BAD,
∴△EAC≌△BAD(SAS),
∴BD=CE.
∵AE=AB=7,
∴BE=![]() ,∠ABE=∠AEB=45°,
,∠ABE=∠AEB=45°,
又∵∠ABC=45°,
∴∠ABC+∠ABE=45°+45°=90°,
∴EC=![]() ,
,
∴BD=CE=![]() .
.
情形2:如图3﹣2中,作AE⊥AB交BC的延长线于E,则△ABE是等腰直角三角形,
同法可证:△EAC≌△BAD(SAS),
∴BD=CE,
∵AB=AE=7,
∴BE=7![]() ,
,
∴EC=BE=CB=7![]() ﹣3,
﹣3,
综上所述,BD的长为![]() 或7
或7![]() ﹣3.
﹣3.
【点睛】
考查了等腰直角三角形的性质,全等三角形的判定和性质,勾股定理等知识,解题的关键是正确寻找全等三角形解决问题,学会用分类讨论的思想思考问题.

 。
。