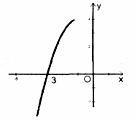
如图，在平面直角坐标系中，抛物线与轴正半轴交于点，且点的坐标为，过点作垂直于轴的直线．是该抛物线上的任意一点，其横坐标为，过点作于点；是直线上的一点，其纵坐标为，以，为边作矩形．

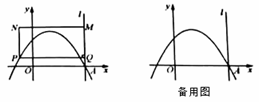
（1）求的值．

（2）当点与点重合时，求的值．

（3）当矩形是正方形，且抛物线的顶点在该正方形内部时，求的值．

（4）当抛物线在矩形内的部分所对应的函数值随的增大而减小时，直接写出的取值范围．

答案

（1）；（2）；（3）；（4）或．

【解析】

（1）将A点坐标代入函数解析式即可求得b的值；

（2）分别表示出P、Q、M的坐标，根据Q、M的横坐标相同，它们重合时纵坐标也相同，列出方程求解即可；

（3）分别表示出PQ和MQ的长度，根据矩形是正方形时，即可求得m的值，再根据顶点在正方形内部，排除不符合条件的m的值；

（4）分，，，四种情况讨论，结合图形分析即可．

【详解】

解：（1）将点代入

得，

解得b=1,；

（2）由（1）可得函数的解析式为，

∴,

∵于点，

∴,

∵是直线上的一点，其纵坐标为，

∴，

若点与点重合，则

，

解得；

（3）由（2）可得，，

当矩形是正方形时，

即，

即或，

解得，

解得，

又，

∴抛物线的顶点为(1，2)，

∵抛物线的顶点在该正方形内部，

∴P点在抛物线对称轴左侧，即，且M点的纵坐标大于抛物线顶点的纵坐标，即，

解得，故m的值为；

（4）①如下图

当时，若抛物线在矩形内的部分所对应的函数值随的增大而减小，

则M点的纵坐标应该小于P点纵坐标，且P点应该在x轴上侧，

即且，

解得，

解得，

∴，

②如下图

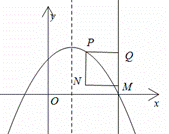
当时，若抛物线在矩形内的部分所对应的函数值随的增大而减小，

则M点的纵坐标应该小于P点纵坐标，

即，解得，

∴；

③当时，P点和M点都在直线x=3上不构成矩形，不符合题意；

④如下图

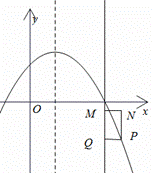
当时，若抛物线在矩形内的部分所对应的函数值随的增大而减小，

则M点的纵坐标应该大于P点纵坐标，

即，解得或，

故，

综上所述或．

【点睛】

本题考查二次函数综合，正方形的性质定理，求二次函数解析式．能分别表示出M、P、Q的坐标并结合图形分析是解决此题的关键，注意分类讨论．