我们不妨约定：若某函数图像上至少存在不同的两点关于原点对称，则把该函数称之为“H函数”，其图像上关于原点对称的两点叫做一对“H点”，根据该约定，完成下列各题

（1）在下列关于x的函数中，是“H函数”的，请在相应题目后面的括号中打“√”，不是“H函数”的打“×”

①（     ）    ②（    ）    ③（   ）

（2）若点与点关于x的“H函数”y=ax²+bx+c(a≠0)的一对“H点”，且该函数的对称轴始终位于直线的右侧，求的值域或取值范围；

（3）若关于x的“H函数” （a，b，c是常数）同时满足下列两个条件：①，②，求该H函数截x轴得到的线段长度的取值范围．

答案

（1）√；√；×；（2）-1＜a＜0，b=4，0＜c＜0；（3）2＜＜2．

【解析】

（1）根据“H函数”的定义即可判断；

（2）先根据题意可求出m,n的取值，代入y=ax²+bx+c(a≠0)得到a,b,c的关系，再根据对称轴在x=2的右侧即可求解；

（3）设“H点”为（p,q）和（-p,-q）,代入得到ap²+3c=0,2bp=q，得到a,c异号，再根据a+b+c=0，代入求出的取值，设函数与x轴的交点为（x₁,0）（x₂,0），t=，利用根与系数的关系得到=，再根据二次函数的性质即可求解．

【详解】

（1）①是 “H函数”②是 “H函数”③不是 “H函数”；

故答案为：√；√；×；

（2）∵A,B是“H点”

∴A,B关于原点对称，

∴m=4,n=1

∴A(1,4），B（-1，-4）

代入y=ax²+bx+c(a≠0)

得

解得

又∵该函数的对称轴始终位于直线的右侧，

∴-＞2

∴-＞2

∴-1＜a＜0

∵a+c=0

∴0＜c＜0，

综上，-1＜a＜0，b=4，0＜c＜0；

（3）∵是“H函数”

∴设H点为（p,q）和（-p,-q）,

代入得

解得ap²+3c=0,2bp=q

∵p²＞0

∴a,c异号，

∴ac＜0

∵a+b+c=0

∴b=-a-c，

∵

∴

∴

∴c²＜4a²

∴＜4

∴-2＜＜2

∴-2＜＜0

设t=，则-2＜t＜0

设函数与x轴的交点为（x₁,0）（x₂,0）

∴x₁, x₂是方程=0的两根

∴

=

=

=

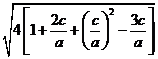
=2

=

又∵-2＜t＜0

∴2＜＜2．

【点睛】

此题主要考查二次函数综合，解题的关键是熟知待定系数法、二次函数的性质及根与系数的关系．