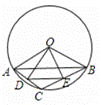
如图,半径为4的![]() 中,弦AB的长度为
中,弦AB的长度为![]() ,点C是劣弧
,点C是劣弧![]() 上的一个动点,点D是弦AC的中点,点E是弦BC的中点,连接DE,OD,OE.
上的一个动点,点D是弦AC的中点,点E是弦BC的中点,连接DE,OD,OE.
(1)求![]() 的度数;
的度数;
(2)当点C沿着劣弧![]() 从点A开始,逆时针运动到点B时,求
从点A开始,逆时针运动到点B时,求![]() 的外心P所经过的路径的长度;
的外心P所经过的路径的长度;
(3)分别记![]() 的面积为
的面积为![]() ,当
,当![]() 时,求弦AC的长度.
时,求弦AC的长度.
(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)过O作OH⊥AB于H,由垂径定理可知AH的长,然后通过三角函数即可得到![]() ,从而可得到
,从而可得到![]() 的度数;
的度数;
(2)连接OC,取OC的中点G,连接DG、EG,可得到O、D、C、E四点共圆,G为△ODE的外心,然后用弧长公式即可算出外心P所经过的路径的长度;
(3)作CN∥AB交圆O于N,作CF⊥AB交AB于F,交DE于P,作OM⊥CN交CN于M,交DE于Q,交AB于H,连接OC,分别表示出![]() ,
,![]() 的面积为
的面积为![]() ,
,![]() ,由
,由![]() 可算出
可算出![]() ,然后可利用勾股定理求出结果.
,然后可利用勾股定理求出结果.
【详解】
解:(1)如图,过O作OH⊥AB于H,
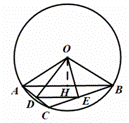
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)如图,连接OC,取OC的中点G,连接DG、EG,
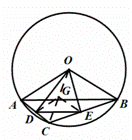
∵D是弦AC的中点,点E是弦BC的中点,![]() ,
,
∴OD⊥AC,OE⊥BC,即∠ODC=∠OEC=90°,
∴![]() ,
,
∴O、D、C、E四点共圆,G为△ODE的外心,
∴G在以O为圆心,2为半径的圆上运动,
∵![]() ,
,
∴运动路径长为![]() ;
;
(3)当点C靠近A点时,如图,作CN∥AB交圆O于N,作CF⊥AB交AB于F,交DE于P,作OM⊥CN交CN于M,交DE于Q,交AB于H,连接OC,
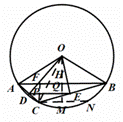
∵D是弦AC的中点,点E是弦BC的中点,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴OH=2,
设![]() ,
,![]() ,由题可知
,由题可知![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]()
![]()
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
解得![]() ,
,
∴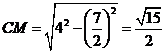 ,即
,即![]() ,
,
由于![]() ,∴
,∴![]() ,
,
又∵![]() ,
,
∴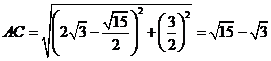 ,
,
同理当点C靠近B点时,可知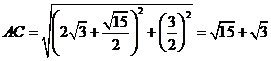 ,
,
综上所述,![]() 或
或![]() .
.
【点睛】
本题是圆的综合问题,题目相对较难,属于中考压轴题类型,理解题意并能准确画出辅助线是解题的关键.
我们不妨约定:若某函数图像上至少存在不同的两点关于原点对称,则把该函数称之为“H函数”,其图像上关于原点对称的两点叫做一对“H点”,根据该约定,完成下列各题
(1)在下列关于x的函数中,是“H函数”的,请在相应题目后面的括号中打“√”,不是“H函数”的打“×”
①![]() ( ) ②
( ) ②![]() ( ) ③
( ) ③![]() ( )
( )
(2)若点![]() 与点
与点![]() 关于x的“H函数”y=ax2+bx+c(a≠0)的一对“H点”,且该函数的对称轴始终位于直线
关于x的“H函数”y=ax2+bx+c(a≠0)的一对“H点”,且该函数的对称轴始终位于直线![]() 的右侧,求
的右侧,求![]() 的值域或取值范围;
的值域或取值范围;
(3)若关于x的“H函数” ![]() (a,b,c是常数)同时满足下列两个条件:①
(a,b,c是常数)同时满足下列两个条件:①![]() ,②
,②![]() ,求该H函数截x轴得到的线段长度的取值范围.
,求该H函数截x轴得到的线段长度的取值范围.
(1)√;√;×;(2)-1<a<0,b=4,0<c<0;(3)2<![]() <2
<2![]() .
.
【解析】
(1)根据“H函数”的定义即可判断;
(2)先根据题意可求出m,n的取值,代入y=ax2+bx+c(a≠0)得到a,b,c的关系,再根据对称轴在x=2的右侧即可求解;
(3)设“H点”为(p,q)和(-p,-q),代入![]() 得到ap2+3c=0,2bp=q,得到a,c异号,再根据a+b+c=0,代入
得到ap2+3c=0,2bp=q,得到a,c异号,再根据a+b+c=0,代入![]() 求出
求出![]() 的取值,设函数与x轴的交点为(x1,0)(x2,0),t=
的取值,设函数与x轴的交点为(x1,0)(x2,0),t=![]() ,利用根与系数的关系得到
,利用根与系数的关系得到![]() =
=![]() ,再根据二次函数的性质即可求解.
,再根据二次函数的性质即可求解.
【详解】
(1)①![]() 是 “H函数”②
是 “H函数”②![]() 是 “H函数”③
是 “H函数”③![]() 不是 “H函数”;
不是 “H函数”;
故答案为:√;√;×;
(2)∵A,B是“H点”
∴A,B关于原点对称,
∴m=4,n=1
∴A(1,4),B(-1,-4)
代入y=ax2+bx+c(a≠0)
得![]()
解得![]()
又∵该函数的对称轴始终位于直线![]() 的右侧,
的右侧,
∴-![]() >2
>2
∴-![]() >2
>2
∴-1<a<0
∵a+c=0
∴0<c<0,
综上,-1<a<0,b=4,0<c<0;
(3)∵![]() 是“H函数”
是“H函数”
∴设H点为(p,q)和(-p,-q),
代入得
解得ap2+3c=0,2bp=q
∵p2>0
∴a,c异号,
∴ac<0
∵a+b+c=0
∴b=-a-c,
∵![]()
∴![]()
∴![]()
∴c2<4a2
∴![]() <4
<4
∴-2<![]() <2
<2
∴-2<![]() <0
<0
设t=![]() ,则-2<t<0
,则-2<t<0
设函数与x轴的交点为(x1,0)(x2,0)
∴x1, x2是方程![]() =0的两根
=0的两根
∴![]()
=![]()
=![]()
=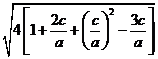
=2![]()
= ![]()
又∵-2<t<0
∴2<![]() <2
<2![]() .
.
【点睛】
此题主要考查二次函数综合,解题的关键是熟知待定系数法、二次函数的性质及根与系数的关系.
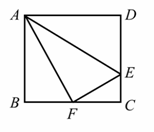
在矩形ABCD中,E为![]() 上的一点,把
上的一点,把![]() 沿AE翻折,使点D恰好落在BC边上的点F.
沿AE翻折,使点D恰好落在BC边上的点F.
(1)求证:![]()
(2)若![]() ,求EC的长;
,求EC的长;
(3)若![]() ,记
,记![]() ,求
,求![]() 的值.
的值.
(1)证明过程见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)只要证明∠B=∠C=90°,∠BAF=∠EFC即可;
(2)因为△AFE是△ADE翻折得到的,得到AF=AD=4,根据勾股定理可得BF的长,从而得到CF的长,根据△ABF∽△FCE,得到![]() ,从而求出EC的长;
,从而求出EC的长;
(3)根据△ABF∽△FCE,得到∠CEF=∠BAF=![]() ,所以tan
,所以tan![]() +tan
+tan![]() =
=![]() ,设CE=1,DE=x,可得到AE,AB,AD的长,根据△ABF∽△FCE,得到
,设CE=1,DE=x,可得到AE,AB,AD的长,根据△ABF∽△FCE,得到![]() ,将求出的值代入化简会得到关于x的一元二次方程,解之即可求出x的值,然后可求出CE,CF,EF,AF的值,代入tan
,将求出的值代入化简会得到关于x的一元二次方程,解之即可求出x的值,然后可求出CE,CF,EF,AF的值,代入tan![]() +tan
+tan![]() =
=![]() 即可.
即可.
【详解】
(1)证明:∵四边形ABCD是矩形,
∴∠B=∠C=∠D=90°,
∴∠AFB+∠BAF=90°,
∵△AFE是△ADE翻折得到的,
∴∠AFE=∠D=90°,
∴∠AFB+∠CFE=90°,
∴∠BAF=∠CFE,
∴△ABF∽△FCE.
(2)解:∵△AFE是△ADE翻折得到的,
∴AF=AD=4,
∴BF=![]() ,
,
∴CF=BC-BF=AD-BF=2,
由(1)得△ABF∽△FCE,
∴![]() ,
,
∴![]() ,
,
∴EC=![]() .
.
(3)
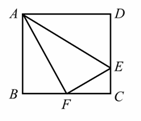
解:由(1)得△ABF∽△FCE,
∴∠CEF=∠BAF=![]() ,
,
∴tan![]() +tan
+tan![]() =
=![]() ,
,
设CE=1,DE=x,
∵![]() ,
,
∴AE=DE+2EC=x+2,AB=CD=x+1,AD=![]()
∵△ABF∽△FCE,
∴![]() ,
,
∴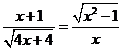 ,
,
∴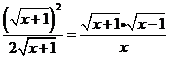 ,
,
∴![]() ,
,
∴![]() ,
,
∴x2-4x+4=0,
解得x=2,
∴CE=1,CF=![]() ,EF=x=2,AF= AD=
,EF=x=2,AF= AD=![]() =
=![]() ,
,
∴tan![]() +tan
+tan![]() =
=![]() =
=![]() .
.
【点睛】
本题考查了相似三角形的判定与性质,翻折变换,矩形的性质,勾股定理等知识.解题的关键是灵活运用所学知识解决问题,学会运用方程的思想思考问题.
今年6月以来,我国多地遭遇强降雨,引发洪涝灾害,人民的生活受到了极大的影响,“一方有难,八方支援”,某市筹集了大量的生活物资,用A,B两种型号的货车,分两批运往受灾严重的地区,具体运算情况如下:
| 第一批 | 第二批 | |
| A型货车的辆数(单位:辆) | 1 | 2 |
| B型货车的辆数(单位:辆) | 3 | 5 |
| 累计运送货物的顿数(单位:吨) | 28 | 50 |
| 备注:第一批、第二批每辆货车均满载 |
(1)求A,B两种型号货车每辆满载分别能运多少吨生活物资;
(2)该市后续又筹集了62.4吨生活物资,现已联系了3辆A型号货车,试问至少还需联系多少辆B型号货车才能一次性将这批生活物资运往目的地.
(1)A,B两种型号货车每辆满载分别能运10吨,6吨生活物资;(2)6.
【解析】
(1)设A,B两种型号货车每辆满载分别能运x,y吨生活物资,根据条件建立方程组求出其解即可;
(2)设还需联系m辆B型号货车才能一次性将这批生活物资运往目的地,根据题中的不等关系列出不等式解答即可.
【详解】
解:(1)设A,B两种型号货车每辆满载分别能运x,y吨生活物资
依题意,得![]() 解得
解得![]()
∴A,B两种型号货车每辆满载分别能运10吨,6吨生活物资
(2)设还需联系m辆B型号货车才能一次性将这批生活物资运往目的地
依题意,得![]() .
.
解得m![]() 5.4
5.4
又m为整数,∴m最小取6
∴至少还需联系6辆B型号货车才能一次性将这批生活物资运往目的地.
【点睛】
本题考查了列二元一次方程组解实际问题的运用,一元一次不等式的运用,解决问题的关键是读懂题意,找到关键描述语,找到所求的量的等量关系.
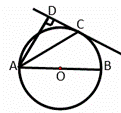
如图,![]() 为
为![]() 的直径,C为
的直径,C为![]() 上的一点,AD与过点C的直线互相垂直,垂足为D,AC平分
上的一点,AD与过点C的直线互相垂直,垂足为D,AC平分![]() .
.
(1)求证:DC为![]() 的切线;
的切线;
(2)若![]() ,求
,求![]() 的半径.
的半径.
(1)详见解析;(2)2
【解析】
(1)连接OC,利用角平分线的性质及同圆半径相等的性质求出∠DAC=∠OCA,得到AD∥OC,即可得到OC⊥CD得到结论;
(2)连接BC,先求出![]() ,得到∠CAB=∠DAC=30°,AC=2CD=
,得到∠CAB=∠DAC=30°,AC=2CD=![]() ,再根据
,再根据![]() 为
为![]() 的直径得到∠ACB=90°,再利用三角函数求出AB.
的直径得到∠ACB=90°,再利用三角函数求出AB.
【详解】
(1)连接OC,
∵OA=OC,
∴∠OAC=∠OCA,
∵AC平分![]() ,
,
∴∠DAC=∠OAC,
∴∠DAC=∠OCA,
∴AD∥OC,
∴∠ADC+∠OCD=180°,
∵AD⊥CD,
∴∠ADC=90°,
∴∠OCD=90°,
∴OC⊥CD,
∴DC为![]() 的切线;
的切线;
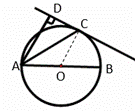
(2)连接BC,
在Rt△ACD中,∠ADC=90°,![]() ,
,
∴![]() ,
,
∴∠DAC=30°,
∴∠CAB=∠DAC=30°,AC=2CD=![]() ,
,
∵AB是![]() 的直径,
的直径,
∴∠ACB=90°,
∴AB=![]() ,
,
∴![]() 的半径为2.
的半径为2.
【点睛】
此题考查角平分线的性质定理,圆的切线的判定定理,圆周角定理,锐角三角函数,直角三角形30°角的性质,正确连接辅助线解题是此题的关键.
本卷还有20题,登录并加入会员即可免费使用哦~

该作品由: 用户李朝阳分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。