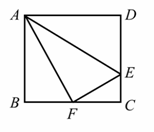
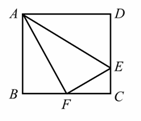
在矩形ABCD中，E为
上的一点，把
沿AE翻折，使点D恰好落在BC边上的点F．
（1）求证：
（2）若
，求EC的长；
（3）若
，记
，求
的值．
答案
（1）证明过程见解析；（2）
；（3）．
【解析】
（1）只要证明∠B=∠C=90°，∠BAF=∠EFC即可；
（2）因为△AFE是△ADE翻折得到的，得到AF=AD=4，根据勾股定理可得BF的长，从而得到CF的长，根据△ABF∽△FCE，得到
，从而求出EC的长；
（3）根据△ABF∽△FCE，得到∠CEF=∠BAF=
，所以tan+tan
=
，设CE=1，DE=x，可得到AE，AB，AD的长，根据△ABF∽△FCE，得到
，将求出的值代入化简会得到关于x的一元二次方程，解之即可求出x的值，然后可求出CE，CF，EF，AF的值，代入tan+tan=
即可．
【详解】
（1）证明：∵四边形ABCD是矩形，
∴∠B=∠C=∠D=90°，
∴∠AFB+∠BAF=90°，
∵△AFE是△ADE翻折得到的，
∴∠AFE=∠D=90°，
∴∠AFB+∠CFE=90°，
∴∠BAF=∠CFE，
∴△ABF∽△FCE．
（2）解：∵△AFE是△ADE翻折得到的，
∴AF=AD=4，
∴BF=
，
∴CF=BC-BF=AD-BF=2，
由（1）得△ABF∽△FCE，
∴，
∴
，
∴EC=．
（3）
解：由（1）得△ABF∽△FCE，
∴∠CEF=∠BAF=，
∴tan+tan=，
设CE=1，DE=x，
∵，
∴AE=DE+2EC=x+2，AB=CD=x+1，AD=
∵△ABF∽△FCE，
∴，
∴
，
∴
，
∴
，
∴
，
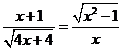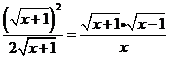∴x2-4x+4=0，
解得x=2，
∴CE=1，CF=
，EF=x=2，AF= AD==
，
∴tan+tan==
．
【点睛】
本题考查了相似三角形的判定与性质，翻折变换，矩形的性质，勾股定理等知识．解题的关键是灵活运用所学知识解决问题，学会运用方程的思想思考问题．
