菱形
的对角线
相交于点O，
，点G是射线
上一个动点，过点G作
交射线
于点E，以
为邻边作矩形
．
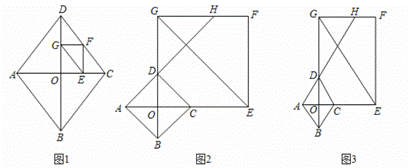
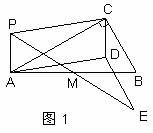
（1）如图1，当点F在线段
上时，求证：
；
（2）若延长
与边
交于点H，将
沿直线翻折180°得到
．
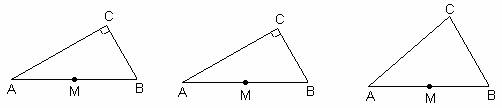
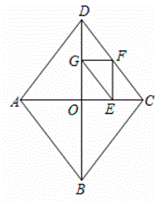
①如图2，当点M在
上时，求证：四边形为正方形：
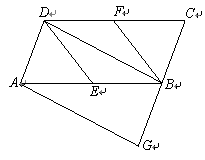
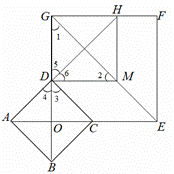
②如图3，当
为定值
时，设
，k为大于0的常数，当且仅当
时，点M在矩形的外部，求m的值．
答案
（1）见解析；（2）①见解析；②
．
【解析】
（1）证明四边形ECFG，DGEF是平行四边形即可得到结论；
（2）①由折叠得
可证明
，
，再证明
可得GO=EO，再由四边形EOGF为矩形则可证明结论；
②由四边形ABCD为菱形以及折叠可得
，当且仅当时，M点在矩形EOGF的外部，
时，M点在矩形EOGF上，即点M在EF上，设
，求得
，过点D作
于点N，证明
求得
，在
中运用勾股定理列出方程
求解即可.
【详解】
（1）证明：如图，
四边形EOGF为矩形，
，
，
，
，
，
四边形ECFG，DGEF是平行四边形，
，
，
；
（2）如图，
证明：由折叠得，
，
，
，，
四边形ABCD为菱形，
，
，
，
，
，
，
，
，
，点M在GE上，
，
，
四边形EOGF为矩形，
矩形EOGF为正方形；
（3）如图，
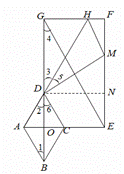
四边形ABCD为菱形，
，
，
，
，
，
，
（m为定值），
，
点M始终在固定射线DM上并随k的增大向上运动，
当且仅当时，M点在矩形EOGF的外部，
时，M点在矩形EOGF上，即点M在EF上，
设，
，
，
，
，
，
，
过点D作于点N，
，又
，
，
，
，
，
，
，
是直角三角形，
，
，
，
（负值舍去），
，
．
【点睛】
本题考查四边形的综合问题，涉及矩形和菱形的性质，勾股定理，锐角三角函数，解方程等知识，综合程度较高，考查学生灵活运用知识的能力．
