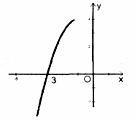
如图，在平面直角坐标系中，是坐标原点，抛物线经过点和点，

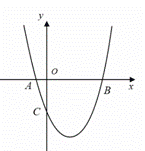
(1)求抛物线的表达式；

(2)如图，线段绕原点逆时针旋转30°得到线段．过点作射线，点是射线上一点(不与点重合)，点关于轴的对称点为点，连接

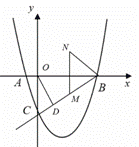
①请直接写出的形状为__________．

②设的面积为的面积为是，当时，求点的坐标；

（3）如图，在（2）的结论下，过点作，交的延长线于点，线段绕点逆时针旋转，旋转角为得到线段，过点作轴，交射线于点，的角平分线和的角平分线相交于点，当时，请直接写出点的坐标为__________．

答案

（1）；（2）①等边三角形；②；（3）（6，）

【解析】

（1）根据题意代入点B、C坐标，利用待定系数法解析式可解；

（2）①过点D作DH⊥OB于点H ，利用解直角三角形知识，求出，得到，由对称性问题可解；

②在①基础上，分别求出S1、S2面积，求出MN则问题可解；

（3）由旋转的性质可知BE=BF，然后根据（2）中的结论可得点E和点F到x轴距离相等，又由于FK ∥x轴，所以点K到x轴的距离等于点F到x轴的距离，从而确定E、K重合，可得为等边三角形，从而根据题目条件可求点G坐标．

【详解】

解：（1）∵抛物线经过点B（6，0），C（0，-3）

∴

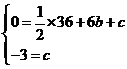
解得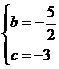

∴抛物线的表达式为．

（2）①等边三角形

如图

过点D作DH⊥OB于点H，

在中，

在中，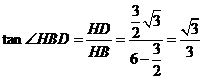

∴

由轴对称可知，，

∴为等边三角形

故答案为：等边三角形；

②由①，得

设

在中，

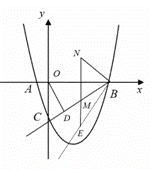
（3）由题意如图，

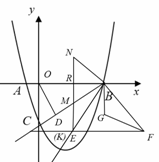
在（2）的结论下可知△BMN为等边三角形，M（3，）

∵，交的延长线于点，

∴∠MBE=30°，ER=

∵线段绕点逆时针旋转，旋转角为得到线段

∴点F到x轴的距离= ER=

∵FK ∥x轴，

∴点K到x轴的距离等于点F到x轴的距离= ER=

又∵点K、E均在射线BE上

∴K、E两点重合

∴

∴为等边三角形

∴，∠OBG=90°

∵

∴点G坐标为（6，）

故答案为：（6，）

【点睛】

本题考查二次函数的综合、待定系数法、旋转的性质、轴对称及等边三角形的性质等知识，综合性较强，利用数形结合思想解题是关键，属于中考压轴题．