小云在学习过程中遇到一个函数![]() .下面是小云对其探究的过程,请补充完整:
.下面是小云对其探究的过程,请补充完整:
(1)当![]() 时,对于函数
时,对于函数![]() ,即
,即![]() ,当
,当![]() 时,
时,![]() 随
随![]() 的增大而 ,且
的增大而 ,且![]() ;对于函数
;对于函数![]() ,当
,当![]() 时,
时,![]() 随
随![]() 的增大而 ,且
的增大而 ,且![]() ;结合上述分析,进一步探究发现,对于函数
;结合上述分析,进一步探究发现,对于函数![]() ,当
,当![]() 时,
时,![]() 随
随![]() 的增大而 .
的增大而 .
(2)当![]() 时,对于函数
时,对于函数![]() ,当
,当![]() 时,
时,![]() 与
与![]() 的几组对应值如下表:
的几组对应值如下表:
|
| 0 |
| 1 |
| 2 |
| 3 |
|
|
| 0 |
|
|
| 1 |
|
|
|
综合上表,进一步探究发现,当![]() 时,
时,![]() 随
随![]() 的增大而增大.在平面直角坐标系
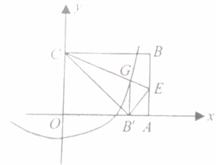
的增大而增大.在平面直角坐标系![]() 中,画出当
中,画出当![]() 时的函数
时的函数![]() 的图象.
的图象.

(3)过点(0,m)(![]() )作平行于
)作平行于![]() 轴的直线
轴的直线![]() ,结合(1)(2)的分析,解决问题:若直线
,结合(1)(2)的分析,解决问题:若直线![]() 与函数
与函数![]() 的图象有两个交点,则
的图象有两个交点,则![]() 的最大值是 .
的最大值是 .
答案
(1)减小,减小,减小;(2)见解析;(3)![]()
【解析】(1)根据一次函数的性质,二次函数的性质分别进行判断,即可得到答案;
(2)根据表格的数据,进行描点,连线,即可画出函数的图像;
(3)根据函数图像和性质,当![]() 时,函数有最大值,代入计算即可得到答案.
时,函数有最大值,代入计算即可得到答案.
【详解】解:(1)根据题意,在函数![]() 中,
中,
∵![]() ,
,
∴函数![]() 在
在![]() 中,
中,![]() 随
随![]() 的增大而减小;
的增大而减小;
∵![]() ,
,
∴对称轴为:![]() ,
,
∴![]() 在
在![]() 中,
中,![]() 随
随![]() 的增大而减小;
的增大而减小;
综合上述,![]() 在
在![]() 中,
中,![]() 随
随![]() 的增大而减小;
的增大而减小;
故答案为:减小,减小,减小;
(2)根据表格描点,连成平滑的曲线,如图:

(3)由(2)可知,当![]() 时,
时,![]() 随
随![]() 的增大而增大,无最大值;
的增大而增大,无最大值;
由(1)可知![]() 在
在![]() 中,
中,![]() 随
随![]() 的增大而减小;
的增大而减小;
∴在![]() 中,有
中,有
当![]() 时,
时,![]() ,
,
∴m的最大值为![]() ;
;
故答案为:![]() .
.
【点睛】本题考查了二次函数的性质,一次函数的性质,以及函数的最值问题,解题的关键是熟练掌握题意,正确的作出函数图像,并求函数的最大值.

 (a,b,c是常数,a≠0),那么y叫做x 的二次函数。
(a,b,c是常数,a≠0),那么y叫做x 的二次函数。  (a,b,c是常数,a≠0);
(a,b,c是常数,a≠0);  (a,h,k是常数,a≠0)
(a,h,k是常数,a≠0)  与x轴有交点时,即对应二次好方程
与x轴有交点时,即对应二次好方程 有实根x1和x2存在时,根据二次三项式的分解因式
有实根x1和x2存在时,根据二次三项式的分解因式 ,二次函数
,二次函数 可转化为两根式
可转化为两根式 。如果没有交点,则不能这样表示。
。如果没有交点,则不能这样表示。