如图![]() 和
和![]() 都是边长为
都是边长为![]() 的等边三角形,它们的边
的等边三角形,它们的边![]() 在同一条直线
在同一条直线![]() 上,点
上,点![]() ,
,![]() 重合,现将
重合,现将![]() 沿着直线
沿着直线![]() 向右移动,直至点
向右移动,直至点![]() 与
与![]() 重合时停止移动.在此过程中,设点移动的距离为
重合时停止移动.在此过程中,设点移动的距离为![]() ,两个三角形重叠部分的面积为
,两个三角形重叠部分的面积为![]() ,则
,则![]() 随
随![]() 变化的函数图像大致为( )
变化的函数图像大致为( )

A. 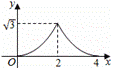 B.
B. 
C. 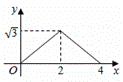 D.
D. 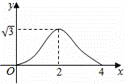
答案
A
【解析】根据图象可得出重叠部分三角形的边长为x,根据特殊角三角函数可得高为![]() ,由此得出面积y是x的二次函数,直到重合面积固定,再往右移动重叠部分的边长变为(4-x),同时可得
,由此得出面积y是x的二次函数,直到重合面积固定,再往右移动重叠部分的边长变为(4-x),同时可得
【详解】C点移动到F点,重叠部分三角形的边长为x,由于是等边三角形,则高为![]() ,面积为y=x·
,面积为y=x·![]() ·
·![]() =
=![]() ,
,
B点移动到F点,重叠部分三角形的边长为(4-x),高为![]() ,面积为
,面积为
y=(4-x)·![]() ·
·![]() =
=![]() ,
,
两个三角形重合时面积正好为![]() .
.
由二次函数图象的性质可判断答案为A,
故选A.
【点睛】本题考查三角形运动面积和二次函数图像性质,关键在于通过三角形面积公式结合二次函数图形得出结论.

 方程有两个不等实数根;
方程有两个不等实数根; 方程有两个相等实数根;
方程有两个相等实数根; 方程没有实数根。
方程没有实数根。 △>0;
△>0; △=0;
△=0; △<0。
△<0。 (△>0)与x轴两交点间的距离的问题。
(△>0)与x轴两交点间的距离的问题。