问题情境:
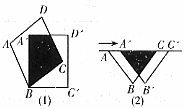
已知AC是正方形ABCD的对角线，将正方形PQST和正方形ABCD按如图放置.
(1)如图1，使点P与点A重合，PT与DC相交与点E, PQ与CB的延长线相交于点F.求证: AF=AE
(2)如图2，使点P在AC上(A, C两点除外)，PT与DC相交与点E, PQ与CB的延长线相交与点F.判断PE和PF的数量关系，并说明理由.
拓广探索:
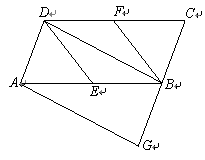
(3) 如图3，使P在BC上(B，C两点除外), PT经过点A, PQ与正方形ABCD的外角∠DCK的平分线CE相交与点E.判断PA和PE的数量关系，并说明理由.
答案
考点：正方形与全等三角形综合
答案：见解析
解析:( 1 )手拉手全等可以证明
MDE≌ABF(AS)
AF=AE
(2)PE=PF ,理由如下:
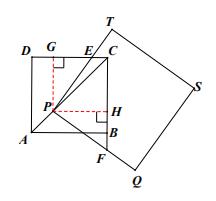
过点P作PG⊥DC于点G,作PH⊥BC于点H
四边形PQST是正方形
∠QPT= 90°
四边形ABCD是正方形
CP平分∠DCB，∠BCD= 90°
又PG⊥DC于点G，PH⊥BC于点H
PG= PH
PG⊥DC，PH⊥BC
∠PGC=90°，∠PHC= 90°
在四边形PHCG中，∠PGC=90°，∠PHC=90°，∠GCH = 90°
∠GPH= 360°-∠PGC-∠GCH- ∠PHC= 360°- 90°- 90°- 90°= 90°
∠GPE+∠EPH =90°
∠QPT= 90°
∠EPH+∠HPF = 90°
∠GPE=∠HPF
PGE≌PHF( ASA)
PE= PF
(3)PA=PE ,理由如下:
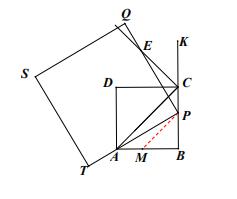
在BA上取点M使得BM=BP,连接PM
四边形PQST是正方形
∠QPT= 90°
∠CPE+∠BPA= 90° .
四边形ABCD是正方形
AB=BC，∠B=90°，∠ BCD= 90°
在ABP中∠B=90°，∠BAP+∠BPA=90°
∠CPE=∠B4P
AB=BC，BM=BP
AB-BM= BC- BP即AM= PC .
∠B=90°，BM=BP
BMP是等腰直角三E角形，∠BMP= 45°
∠AMP=180°-∠BMP= 180°- 45°= 135°
CE平分∠DCK
∠DCE=
∠DCK=45° .
∠PCE=∠PCD+∠DCE=90° +45°= 135°
∠AMP=∠PCE
∠CPE=∠BAP，AM=PC，∠AMP=∠PCE
AMP≌PCE(ASA)
PA=PE
