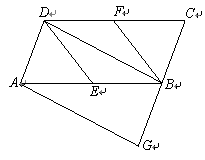
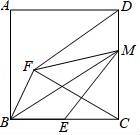
如图，正方形ABCD中，AB＝2，E是BC中点，CD上有一动点M，连接EM、BM，将△BEM沿着BM翻折得到△BFM．连接DF、CF，则DF+
FC的最小值为_________．
答案
．
【分析】取BG＝
，连接FG，首先证明△BGF∽△BFC，从而可得到FG＝
FC，然后依据三角形的三边关系可知DF+
FC＝DF+FC≤DG，然后依据勾股定理求得DG的值即可．
【解答】解：如图所示：取BG＝，连接FG．
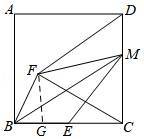
∵BC＝2，E是BC的中点，
∴BE＝1．
由翻折的性质可知BF＝BE＝1．
∵BF＝1，BC＝2，GB＝，
∴BF2＝BC•GB．
∴
．
又∵∠FBG＝∠FBC，
∴△BGF∽△BFC，
∴
＝
＝
，
∴FG＝FC．
∴DF+FC＝DF+FC≤DG＝
＝
＝
．
∴DF+FC的最小值为．
