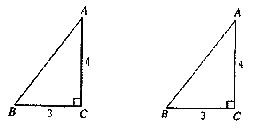
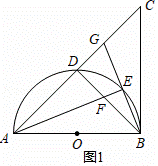
如图，在△ABC中，BA＝BC，∠ABC＝90°，以AB为直径的半圆O交AC于点D，点E是
上不与点B，D重合的任意一点，连接AE交BD于点F，连接BE并延长交AC于点G．
（1）求证：△ADF≌△BDG；
（2）填空：
①若AB＝4，且点E是
的中点，则DF的长为 4﹣2
；
②取
的中点H，当∠EAB的度数为 30° 时，四边形OBEH为菱形．
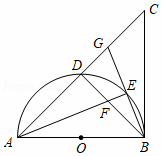
答案
解：（1）证明：如图1，∵BA＝BC，∠ABC＝90°，
∴∠BAC＝45°
∵AB是⊙O的直径，
∴∠ADB＝∠AEB＝90°，
∴∠DAF+∠BGD＝∠DBG+∠BGD＝90°
∴∠DAF＝∠DBG
∵∠ABD+∠BAC＝90°
∴∠ABD＝∠BAC＝45°
∴AD＝BD
∴△ADF≌△BDG（ASA）；
（2）①如图2，过F作FH⊥AB于H，∵点E是
的中点，
∴∠BAE＝∠DAE
∵FD⊥AD，FH⊥AB
∴FH＝FD
∵
＝sin∠ABD＝sin45°＝
，
∴
，即BF＝
FD
∵AB＝4，
∴BD＝4cos45°＝2，即BF+FD＝2
，（+1）FD＝2
∴FD＝
＝4﹣2
故答案为
．
②连接OE，EH，∵点H是
的中点，
∴OH⊥AE，
∵∠AEB＝90°
∴BE⊥AE
∴BE∥OH
∵四边形OBEH为菱形，
∴BE＝OH＝OB＝
AB
∴sin∠EAB＝
＝
∴∠EAB＝30°．
故答案为：30°
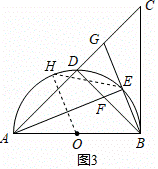
【点评】本题主要考查了圆的性质，垂径定理，等腰直角三角形的性质，菱形的性质，解直角三角形，特殊角的三角函数值等，关键在灵活应用性质定理．
