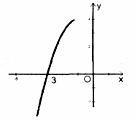
如图，正比例函数和反比例函数的图象都经过点A（3，3），把直线OA向下平移后，与反比例函数的图象交于点B（6，m），与x轴、y轴分别交于C、D两点．

（1）求m的值；

（2）求过A、B、D三点的抛物线的解析式；

（3）若点E是抛物线上的一个动点，是否存在点E，使四边形OECD的面积S₁，是四边形OACD面积S的？若存在，求点E的坐标；若不存在，请说明理由．

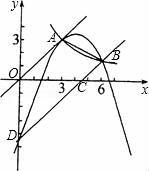
答案

解：（1）∵反比例函数的图象都经过点A（3，3），

∴经过点A的反比例函数解析式为：y＝，

而直线OA向下平移后，与反比例函数的图象交于点B（6，m），

∴m＝＝；

（2）∵直线OA向下平移后，与反比例函数的图象交于点B（6，），

与x轴、y轴分别交于C、D两点，

而这些OA的解析式为y＝x，

设直线CD的解析式为y＝x+b，

代入B的坐标得：＝6+b，

∴b＝﹣4.5，

∴直线OC的解析式为y＝x﹣4.5，

∴C、D的坐标分别为（4.5，0），（0，﹣4.5），

设过A、B、D三点的抛物线的解析式为y＝ax²+bx+c，

分别把A、B、D的坐标代入其中得：

，

解之得：a＝﹣0.5，b＝4，c＝﹣4.5

∴y＝﹣0.5x²+4x﹣4.5；

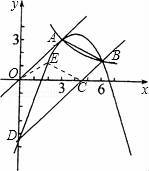
（3）如图，设E的横坐标为x，

∴其纵坐标为﹣0.5x²+4x﹣4.5，

∴S₁＝（﹣0.5x²+4x﹣4.5+OD）×OC，

＝（﹣0.5x²+4x﹣4.5+4.5）×4.5，

＝（﹣0.5x²+4x）×4.5，

而S＝（3+OD）×OC＝（3+4.5）×4.5＝，

∴（﹣0.5x²+4x）×4.5＝×，

解之得x＝4±，

∴这样的E点存在，坐标为（4﹣，0.5），（4+，0.5）．

【点评】本题考查点的坐标的求法及利用待定系数法确定二次函数解析式．此题也为数学建模题，借助一元二次方程解决探究问题．