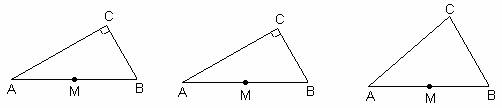
我们知道定理“直角三角形斜边上的中线等于斜边的一半”，这个定理的逆命题也是真命题．
（1）这个定理的逆命题是 ；
（2）下面我们来证明这个逆命题：
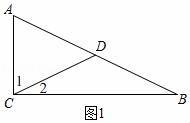
已知：如图1，CD是△ABC的中线，CD=
AB
求证：△ABC为直角三角形．
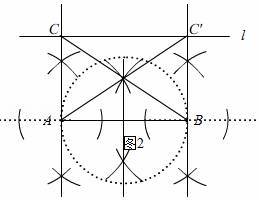
（3）如图2已知线段AB和直线l，点C是直线l上一点，若△ABC为直角三角形，请你用圆规和没有刻度的直尺确定点C位置．
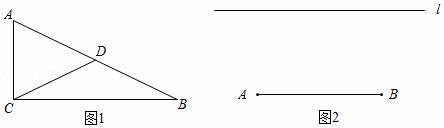
答案
解：（1）∵“直角三角形斜边上的中线等于斜边的一半”，
∴它逆命题是：如果一个三角形一边上的中线等于这条边的一半，那么这个三角形是直角三角形，
故答案为：如果一个三角形一边上的中线等于这条边的一半，那么这个三角形是直角三角形；
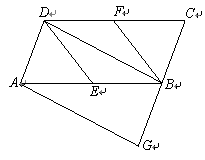
（2）如图，
∵CD是△ABC的中线，
∴AD=BD=
AB，
∵CD=AB，
∴AD=CD=BD，
∴∠A=∠1，∠B=∠2，
在△ABC中，∠A+∠B+∠1+∠2=180°，
∴∠1+∠2+∠1+∠2=180°，
∴∠1+∠2=90°，
∴∠ACB=90°，
∴△ABC为直角三角形；
（3）如图2所示，△ABC和△ABC'为所求作的图形，
