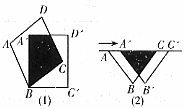
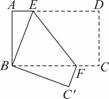
如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点C处,折痕为EF.(1)求证:B=Bf;(2)若∠AB=20^∘,求∠BB∈的度数;(3)若AB=θ,AD=8,求AE的长

当前位置：

学科首页

八下第十八章平行四边形

特殊的平行四边形

试题详情

难度：

使用次数：86

更新时间：2021-04-28

纠错

如图，将矩形纸片ABCD折叠，使点D与点B重合，点C落在点C′处，折痕为EF.

(1)求证：BE＝BF；

(2)若∠ABE＝20°，求∠BFE的度数；

(3)若AB＝6，AD＝8，求AE的长．

查看答案

题型：解答题

知识点：特殊的平行四边形

下载试题

复制试题

【答案】

解：(1)由题意得∠BEF＝∠DEF.∵四边形ABCD为矩形，∴DE∥BF，∴∠BFE＝∠DEF，∴∠BEF＝∠BFE，∴BE＝BF　(2)∵四边形ABCD为矩形，∴∠ABF＝90°；而∠ABE＝20°，∴∠EBF＝90°－20°＝70°；又∵∠BEF＝∠BFE，∴∠BFE的度数为55°　(3)由题意知BE＝DE；设AE＝x，则BE＝DE＝8－x，由勾股定理得(8－x)²＝6²＋x²，解得x＝，即AE的长为

考点梳理:

根据可圈可点权威老师分析，试题“ ”主要考查你对矩形，矩形的性质，矩形的判定等考点的理解。关于这些考点的“资料梳理”如下：

◎ 矩形，矩形的性质，矩形的判定的定义

矩形:
是一种平面图形，矩形的四个角都是直角，同时矩形的对角线相等，而且矩形所在平面内任一点到其两对角线端点的距离的平方和相等。

◎ 矩形，矩形的性质，矩形的判定的知识扩展

1、矩形的定义：有一个角是直角的平行四边形叫做矩形。
2、矩形的性质：（1）具有平行四边形的一切性质
（2）矩形的四个角都是直角
（3）矩形的对角线相等
（4）矩形是轴对称图形，也是中心对称图形。
3、矩形的判定：（1）定义：有一个角是直角的平行四边形是矩形
（2）定理1：有三个角是直角的四边形是矩形
（3）定理2：对角线相等的平行四边形是矩形
4、矩形的面积：S_矩形=长×宽=ab。

◎ 矩形，矩形的性质，矩形的判定的特性

矩形的性质：
1．矩形的4个内角都是直角；
2．矩形的对角线相等且互相平分；
3．矩形所在平面内任一点到其两对角线端点的距离的平方和相等；
4．矩形既是轴对称图形，也是中心对称图形（对称轴是任何一组对边中点的连线），它至少有两条对称轴。对称中心是对角线的交点。
5．矩形是特殊的平行四边形，矩形具有平行四边形的所有性质
6.顺次连接矩形各边中点得到的四边形是菱形

◎ 矩形，矩形的性质，矩形的判定的知识点拨

矩形的判定：
①定义：有一个角是直角的平行四边形是矩形
②定理1：有三个角是直角的四边形是矩形
③定理2：对角线相等的平行四边形是矩形
④对角线互相平分且相等的四边形是矩形
矩形的面积：S_矩形=长×宽=ab。

◎ 矩形，矩形的性质，矩形的判定的知识拓展

黄金矩形:
宽与长的比是（√5-1）/2（约为0.618）的矩形叫做黄金矩形。
黄金矩形给我们一协调、匀称的美感。世界各国许多著名的建筑，为取得最佳的视觉效果，都采用了黄金矩形的设计。如希腊的巴特农神庙等。

◎ 矩形，矩形的性质，矩形的判定的教学目标

1、掌握矩形的性质，判定，并能够运用综合法和严密的数学语言进行推理论证。
2、经历探索、猜测、证明的过程，发展学生的推理论证能力。
3、通过独立完成证明的过程，体会数学是严谨的科学，增强学生对待科学的严谨治学态度，从而养成良好的习惯。

◎ 矩形，矩形的性质，矩形的判定的考试要求

能力要求：掌握
课时要求：130
考试频率：常考
分值比重：7

开通会员

登录并加入会员可无限制查看知识点解析

类题推荐：

特殊的平行四边形

难度：

使用次数：131

更新时间：2021-07-14

加入组卷

如图（1），将边长为2cm的两个互相重合的正方形纸片按住其中一个不动，另一个绕点B顺时针旋转一个角度，若使重叠部分的面积为，则这个旋转角度为______度。如图（2），将上述两个互相重合的正方形纸片沿对角线AC翻折成等腰直角三角形后，再抽出其中一个等腰直角三角形沿AC移动，若重叠部分△A’PC的面积是1cm²，则它移动的距离AA’等于_______cm。