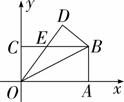
如图,在平面直角坐标系中,长方形OABC的顶点A,C分别在x轴、y轴的正半轴上,点B的坐标为(8,4),将该长方形沿OB翻折,点A的对应点为点D,OD与BC交于点E.
(Ⅰ)证明:EO=EB;
(Ⅱ)求点E的坐标;
(Ⅲ)点M是OB上任意一点,点N是OA上任意一点,是否存在点M、N,使得AM+MN最小?若存在,求出其最小值;若不存在,请说明理由.
答案
解:(Ⅰ)∵将该长方形沿OB翻折,点A的对应点为点D,OD与BC交于点E.
∴∠DOB=∠AOB,
∵BC∥OA,
∴∠OBC=∠AOB,
∴∠OBC=∠DOB,
∴EO=EB;
(Ⅱ)由(Ⅰ)有,EO=EB,
∵长方形OABC的顶点A,C分别在x轴、y轴的正半轴上,点B的坐标为(8,4),
设OE=x,则DE=8-x,
在Rt△BDE中,BD=4,根据勾股定理得,DB2+DE2=BE2,
∴16+(8-x)2=x2,
∴x=5,
∴BE=5,
∴CE=3,
∴E(3,4);
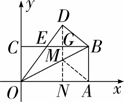
(Ⅲ)如解图,过点D作OA的垂线交OB于M,交OA于N,此时的M,N是AM+MN的最小值的位置,求出DN就是AM+MN的最小值,
由(Ⅱ)有,DE=3,BE=5,BD=4,
∴根据面积有DE×BD=BE×DG,
∴DG=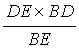 =
=![]() ,
,
由题意有,GN=OC=4,
∴DN=DG+GN=![]() +4=
+4=![]() .
.
即:AM+MN的最小值为![]() .
.

 方程有两个不等实数根;
方程有两个不等实数根; 方程有两个相等实数根;
方程有两个相等实数根; 方程没有实数根。
方程没有实数根。 △>0;
△>0; △=0;
△=0; △<0。
△<0。 (△>0)与x轴两交点间的距离的问题。
(△>0)与x轴两交点间的距离的问题。