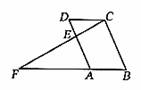
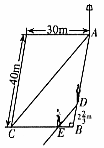
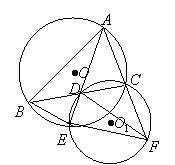
如图,已知A(－3,0),C(0,
),点B在x轴正半轴上,且OB=
OA.
(Ⅰ)求出∠ABC的度数;
(Ⅱ)若点M、N同时从B点出发,均以每秒1个单位长度的速度分别沿BA、BC边运动,其中一个点到达终点时,另一个点也随之停止运动,当运动时间为t秒时,连接MN,将△BMN沿MN翻折,B点恰好落在AC边上的P处,求t的值;
(Ⅲ)在(Ⅱ)的情况下,直接写出点P的坐标.
第2题图
答案
解:(Ⅰ)∵A(－3,0),C(0,),
∴OA=3,OC=,
点B在x轴正半轴上,且OB=OA.
∴OB=1,
∴tan∠ABC＝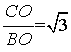
,
∴∠ABC=60°;
(Ⅱ)∵OA=3,OB=1,OC=,
∴BC=2,AB=4,
∴∠B=60°,BM=BN,
∴△BMN是等边三角形,
∴△PMN也是等边三角形,
∴PN=BN=t,∠PNM=∠NMB=60°,
∴PN∥AB,
∴
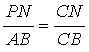,即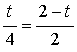
,
∴t=
;
(Ⅲ)P点的坐标是(−1,
).
【解法提示】如解图,过点P作PD⊥AB,垂足为D,
∵t=,
∴BM=PM=,∠PMD=∠CBA=60°,
∴PD=,DM=
,
∴OD=1,
∴P点的坐标是(−1,).
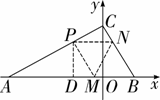
第2题解图
