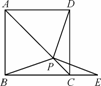
如图,在正方形ABCD中,P是对角线AC上的一点,连接BP,![]() DP,延长BC到E,使PE=PB.求证:∠PDC=∠PEC.
DP,延长BC到E,使PE=PB.求证:∠PDC=∠PEC.
答案
证明:∵四边形ABCD是正方形,
∴BC=CD,∠BCP=∠DCP.
在△BCP和△DCP中,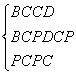 ,
,
∴△BCP≌△DCP(SAS).
∴∠PDC=∠PBC.
∵PE=PB,
∴∠PBC=∠PEC.
∴![]() ∠PDC=∠PEC.
∠PDC=∠PEC.
如图,在正方形ABCD中,P是对角线AC上的一点,连接BP,![]() DP,延长BC到E,使PE=PB.求证:∠PDC=∠PEC.
DP,延长BC到E,使PE=PB.求证:∠PDC=∠PEC.

证明:∵四边形ABCD是正方形,
∴BC=CD,∠BCP=∠DCP.
在△BCP和△DCP中, ,
,
∴△BCP≌△DCP(SAS).
∴∠PDC=∠PBC.
∵PE=PB,
∴∠PBC=∠PEC.
∴![]() ∠PDC=∠PEC.
∠PDC=∠PEC.
矩形的性质:
1.矩形的4个内角都是直角;
2.矩形的对角线相等且互相平分;
3.矩形所在平面内任一点到其两对角线端点的距离的平方和相等;
4.矩形既是轴对称图形,也是中心对称图形(对称轴是任何一组对边中点的连线),它至少有两条对称轴。对称中心是对角线的交点。
5.矩形是特殊的平行四边形,矩形具有平行四边形的所有性质
6.顺次连接矩形各边中点得到的四边形是菱形
登录并加入会员可无限制查看知识点解析