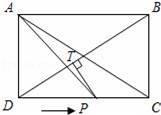
如图，在矩形ABCD中，AD=60cm，CD=80cm，连接AC、BD．动点P从点D出发，以5cm/s速度沿边DC匀速向点C运动，到达点C即停止，过点P作BD的垂线，垂足为T．设点P运动的时间为t s．

（1）当AP⊥BD时，AP的长是多少？

（2）设△APT面积为y（cm²），求y与t之间的函数关系式？并写出自变量t的取值范围；

（3）在P点的运动过程中，△APT的面积能否达到矩形ABCD面积的？若能达到，求出此时t的值；若不能，说明理由．

答案

【考点】相似形综合题．

【分析】（1）先根据勾股定理求出BD，再证明△APD∽△BDA，得出比例式，即可求出AP；

（2）分两种情况：①当0＜t＜9时，点T位于△AOP的内部时，作AG⊥BD于G；先证明△DPT∽△DBC，得出对应边成比例，即，得出DT=4t，PT=3t；再由AD•AB=BD•AG，求出AG=48，S_△APT=S_△AOP﹣S_△ATO﹣S_△OTP=×60×5t﹣×4t×48﹣×4t×3t，即可得出y与t的函数关系式；

②当9＜t≤16时，点T位于△AOP的外部时，由①得：S_△APT=S_△ATO+S_△OTP﹣S_△AOP=6t²﹣54t，即可得出结果；

（3）当t=9时，A，T，P三点在一条直线上，点A，T，P不构成三角形；分两种情况：①当0＜t＜9时，列出方程求解看有无实数根即可；

②当9＜t≤16时，列出方程求解看有无实数根即可．

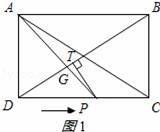
【解答】解：（1）当AP⊥BD时，垂足为G，如图1所示：

则∠BGAD=90°，

∴∠BAG+∠ABD=90°，

∵四边形ABCD是矩形，

∴AB=CD=80cm，∠BAD=∠ADP=90°，

∴BD===100，∠BAG+∠DAP=90°，

∴∠DAP=∠ABD，

∴△APD∽△BDA，

∴，即，

∴AP=75；

（2）当A，T，P三点在一条直线上，点A，T，P不构成三角形，

此时，PD==45，t==9；

∴分两种情况：

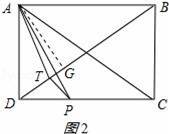
①当0＜t＜9时，点T位于△AOP的内部，如图2所示：

作AG⊥BD于G；

∵PT⊥BD，

∴∠PTD=90°，

∴∠PTD=∠BCD=90°，

又∵∠PDT=∠BDC，

∴△DPT∽△DBC，

∴，即，

∴DT=4t，PT=3t；

由AD•AB=BD•AG，可得：AG=48，

∴S_△APT=S_△AOP﹣S_△ATO﹣S_△OTP

=×60×5t﹣×4t×48﹣×4t×3t

=﹣6t²+54t，

∴y=﹣6t²+54t；

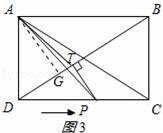
②当9＜t≤16时，点T位于△AOP的外部时，如图3所示：

作AG⊥BD于G，

此时S_△APT=S_△ATO+S_△OTP﹣S_△AOP=6t²﹣54t，

∴y=6t²﹣54t；

综上所述：当0＜t＜9时，y=﹣6t²+54t；当9＜t≤16时，y=6t²﹣54t；

（3）不能；理由如下：

∵矩形ABCD的面积=80×60=4800，若S_△APT=S_矩形ABCD=1200，

①当0＜t＜9时，﹣6t²+54t=1200，即t²﹣9t+200=0．

此时，△=（﹣9）²﹣4×1×200＜0，

∴该方程无实数根．

∴当0＜t＜9时，以A，P，T为顶点的△APT的面积不能达到矩形ABCD面积的；

②当9＜t≤16时，6t²﹣54t=1200，即t²﹣9t﹣200=0．

解得：t=（负值舍去），

∵881＞625=25²，

∴t=＞=17，

而此时9＜t≤16，

∴t=也不符合题意，应舍去．

∴当9＜t≤16时，以A，P，T为顶点的△APT的面积也不能达到矩形ABCD面积的；

综上所述，以A，P，T为顶点的△APT的面积不能达到矩形ABCD面积的．

【点评】本题是相似形综合题，考查了矩形的性质、勾股定理、相似三角形的判定与性质、三角形面积的计算方法、一元二次方程的解法等知识；本题难度较大，综合性强，特别是（2）（3）中，需要通过作辅助线和分类讨论的方法，通过证明三角形相似和解方程才能得出结果．