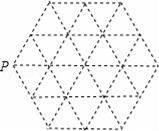
如图,在由24个边长都为1的小正三角形组成的正六边形网格中,以格点P为直角顶点作格点直角三角形(即顶点均在格点上的三角形),请你写出所有可能的直角三角形斜边的长 .

答案
4,2,![]()
![]() ,
,![]()
![]() .
.
【考点】勾股定理;等边三角形的性质;勾股定理的逆定理.
【专题】压轴题;网格型.
【分析】在正六边形网格中,首先找出以点P为直角的直角三角形,然后应用勾股定理求其斜边长.
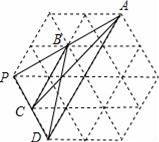
【解答】解:通过作图,知以点P为直角的三角形由四种情况,
如上图,△PCB、△PCA、△PDB、△PDA,均是以点P为直角的直角三角形,
故:在Rt△PCB中,BC=![]()
![]() =
=![]()
![]() =2;
=2;
在Rt△PCA中,AC=![]()
![]() =
=![]()
![]() =
=![]()
![]() ;
;
在Rt△PDB中,BD=![]()
![]() =
=![]()
![]() =
=![]()
![]() ;
;
在Rt△PAD中,AD=![]()
![]() =
=![]()
![]() =4.
=4.
故所有可能的直角三角形斜边的长为4,2,![]()
![]() ,
,![]()
![]() .
.

【点评】本题主要考查勾股定理的应用,难易程度适中.

 。
。