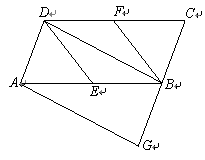
在正方形ABCD中,E为边CD上一点,连接BE.
(1)请你在图1画出△BEM,使得△BEM与△BEC关于直线BE对称;
(2)若边AD上存在一点F,使得AF+CE=EF,请你在图2中探究∠ABF与∠CBE的数量关系并证明;
(3)在(2)的条件下,若点E为边CD的三等分点,且CE<DE,请写出求cos∠FED的思路.(可以不写出计算结果).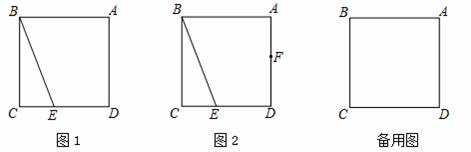
答案
(1)补全图形,如图1所示.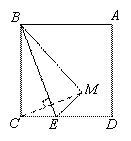
(2)![]() 与
与![]() 的数量关系:
的数量关系:![]() .
.
证明:连接![]() ,
,![]() ,延长
,延长![]() 到
到![]() ,使得
,使得![]() ,连接
,连接![]() .
.
∵四边形![]() 为正方形,
为正方形,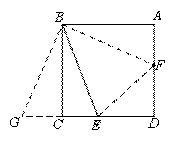
∴![]() ,
,![]() .
.
∴△![]() ≌△
≌△![]() .
.
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() . ∴△
. ∴△![]() ≌△
≌△![]() .
.
∴∠![]() =∠
=∠![]() .
.
∴![]() .
.
(3)求解思路如下:
a.设正方形的边长为![]() ,
,![]() 为
为![]() ,则
,则![]() ,
,![]() ;
;
b.在Rt△![]() 中,由
中,由![]() ,可得
,可得![]()
从而得到![]() 与
与![]() 的关系
的关系![]() ;
;
c.根据cos∠FED![]() ,可求得结果.
,可求得结果.